2019年5月14日，图灵奖得主、多伦多大学教授Geoffrey Hinton远程为北京大学前沿计算中心的师生带来了一场题为“Deep Belief Network”（深度信念网络）的精彩学术讲座。本次报告由中心主任John Hopcroft教授主持，听众主要为北京大学及其他兄弟单位的师生。

　　

　　在机器学习领域，Geoffrey Hinton教授鼎鼎大名，他被称为“深度学习之父”，他于2006年对深度信念网络训练方法的研究成为深度学习领域崛起的标志性工作，直接推动了深度学习方法近年来的飞速发展与普及，为整个人工智能领域的发展做出了巨大的贡献。

　　

　　本次讲座中，Geoffrey Hinton教授就为我们带来了他最核心的深度学习方向研究工作——“Deep Belief Network”，即深度信念网络，该模型为深度学习领域的奠基工作。Hinton教授从一般形式的信念网络开始，介绍了信念网络模型学习中遇到的难题，通过逐步引入玻尔兹曼机（Boltzmann Machine）乃至受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）作为信念网络每一层的模型，最终通过堆叠RBM得到了易于学习的深度信念网络模型。在讲解DBN训练方法的过程中，Hinton教授详细介绍了利用未标记数据逐层无监督预训练，最后通过少量标记数据对模型进行监督训练的深度神经网络训练方法，而该方法即为使得早期深度网络易于训练，从而打败传统浅层优化模型的关键算法，至今仍深刻影响着深度学习领域的研究。

　　

　　Belief Network（信念网络）

　　Hinton教授从最简单的随机二值神经元（Stochastic binary neurons）模型讲起，从概率的角度构建神经网络模型的基本单元——神经元（Neuron），每个神经元表示一个随机变量。而通过带权有向边将每个随机变量的结点连接为一个有向图，即为信念网络（Belief Nets，BN）模型。

　　

　　

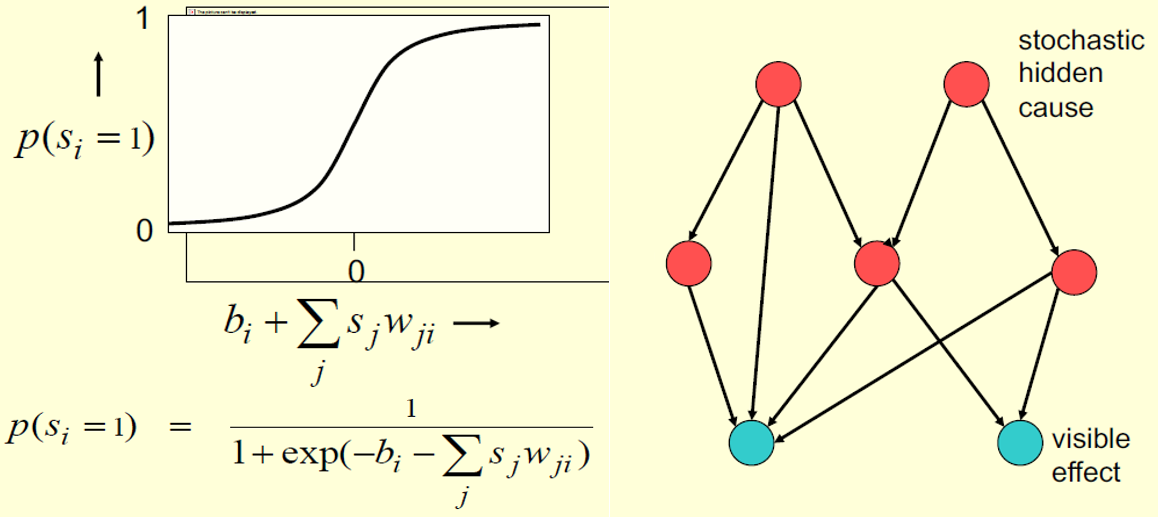
　　虽然通过BN可以容易地从其叶子结点生成无偏的结果（Effect）样本，即网络所“相信”的数据，但要想对所有可能的隐含起因（Cause）状态组合来推断其后验概率却很困难，甚至想从其后验概率中得到一个采样数据都很难，这使得拥有大量参数的深度信念网络模型（Deep Belief Nets，DBN）难以学习。唯有得到对于观测数据的隐含状态后验概率，信念网络的学习才会变得容易。

　　

　　接下来，Hinton教授详细讨论了Sigmoid信念网络的具体学习策略。每一个神经元的训练策略为，优化模型参数w以最大化能够生成训练样本中该单元二值状态的父单元二值状态的采样对数概率（log probability）。参数更新策略如下：

　　

　　

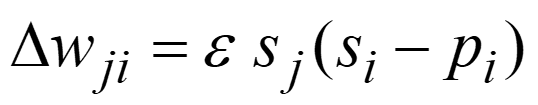
　　但该方法依然存在Explaining Away的问题。Explaining Away是指，即使两个隐含起因变量之间是相互独立的，他们依然会由于所共同决定的结果变量而变得相互关联。除此之外，后验概率（Posterior）除了依赖于先验概率（Prior），同时也依赖于似然度（Likelihood）。这使得学习某一层的参数w时，还需要知道更高层的参数，即不同层的参数之间是相互作用的。而估计第一个隐层的先验概率也十分困难。综合这几点，Hinton教授指出，对Sigmoid Belief Nets进行逐层训练的确是困难的。

　　

　　Boltzmann Machine（玻尔兹曼机）

　　而除了像Sigmoid Belief Net这种利用有向无环图来连接二值随机神经元的方式，Hinton教授在1983年便已经提出了另一种生成式神经网络的模型，即Boltzmann Machine，该模型通过对称带权的边（即无向边）来连接二值随机神经元。

　　

　　

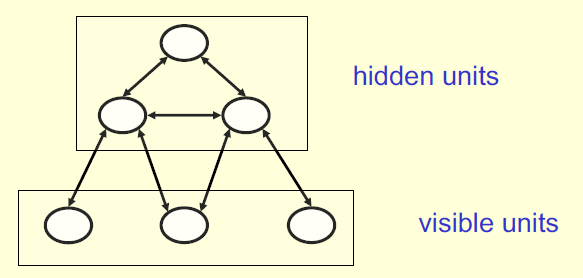
　　Hinton教授给出了Boltzmann Machine的能量函数（Energy Function）的定义：

　　

　　

　　以及每个神经元状态变化对于全局能量的影响：

　　

　　

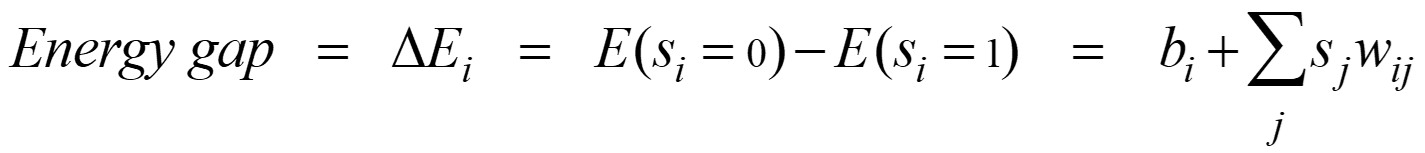
　　为了从Boltzmann Machine中生成样本，只需要不断地根据每个单元的后验概率p(s_i=1)更新其状态即可，p(s_i=1)的定义同前图中随机神经元的定义一致。这样得到的全局状态的概率正比于exp(-E)。

　　

　　而Boltzmann Machine的学习目标为最大化生成训练集中的可见二值状态的联合概率，这与按照如下方式获得N个训练样本向量的概率是等价的：

　　

　　1. 在没有外部输入的前提下，使得网络N次达到平稳分布（stationary distribution）；

　　2. 每次采样得到一个可见的样本向量。

　　

　　但由于两个隐含单元的权重之间相互依赖，使得Boltzmann Machine的学习变得困难。因此，Hinton教授进一步限制了神经元之间的连接，保证同一层隐含单元之间没有连接存在，这就是受限玻尔兹曼机（RBM）。

　　

　　Restricted Boltzmann Machine（RBM，受限玻尔兹曼机）

　　由于隐含单元的状态之间没有相互依赖关系，RBM相比于有向信念网络在后验概率采样上具有极大优势。

　　

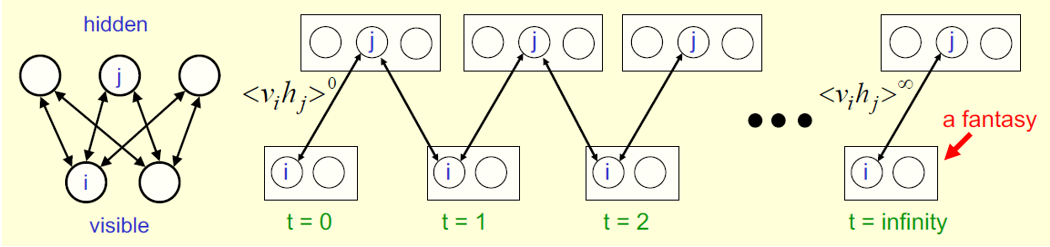
左：RBM；右：Maximum likelihood learning algorithm for an RBM

　　

　　RBM可以通过一种轮流更新隐含单元与可见单元参数的迭代方式进行学习，更新公式如下：

　　

　　

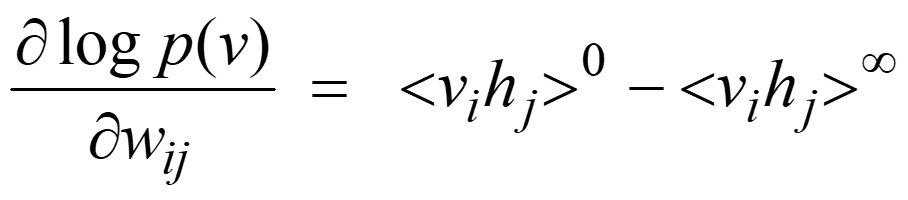
　　但实际中，常常通过一种更为迅速的方式进行RBM的学习，这种方法类似于Contrastive Divergence Learning，虽然没有计算真正的log likelihood，但仍是其他一种目标函数的梯度更新的近似。

　　

　　

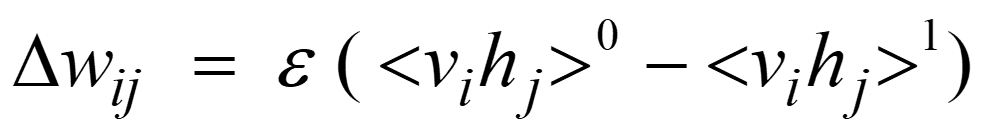
　　通过将多层RBM堆叠起来，即可搭建一个深度的神经网络，这种深度信念网络可以通过逐层的方式训练。第一层RBM直接输入数据特征，而第二层则将第一层的输出视为输入特征，后面的层也重复该计算过程。可以证明，在网络中每增加一层RBM，便会提高训练数据log likelihood的variational lower bound。以上即为单层RBM的学习过程，由于没有用到标记数据，而是通过一种无监督的方式对网络进行预训练，因此称为神经网络的“预训练”方法。

　　

　　在预训练后，即可以通过增加一个输出层来用反向传播的方式来判别式地对网络进行精细调整“Fine-tuning”。相比于直接用反向传播的方式对网络进行训练，这种方式能够克服很多训练中遇到的困难。预训练可以使得网络的参数先达到一种较为合理的区间，即获得一种相对较好的初始值，这样在判别式后处理的过程中只需要进行局部搜索即可达到较优的参数值。

　　

　　最后，Hinton教授总结到，RBM提供了一种简单的无监督学习方式来对网络进行预训练，使得进一步的判别式微调效果更好。这种无监督的训练方式对于解决当前领域内难题仍然具有很大的价值，毕竟大部分数据都缺乏标记，且目前并没有得到充分利用。近年来，已经有工作注意到无监督学习的价值，如BERT，已经在网络学习中引入类似机制。Hinton教授相信在深度学习领域今后的发展中，类似的思想会得到越来越多的重视，发挥更大的作用。

　　

　　以上即为对Hinton教授本次讲座的总结，由于Hinton教授的讲座中涉及较多较为复杂的数学内容，有很多小编并没有理解透彻，经Hinton教授授权，在此将报告的Slides附上以方便大家学习，点击本文附件即可下载。