本文是发表在 IEEE Transactions on Information Theory 上的论文 A Quantum Algorithm Framework for Discrete Probability Distributions With Applications to Rényi Entropy Estimation 的详细解读。该项研究由北京大学李彤阳课题组与腾讯量子实验室张胜誉老师合作完成，北京大学博士生王昕兆为第一作者。

      论文提出了一种基于量子奇异值变换的估计离散概率分布统计性质的框架，并证明其在Rényi熵估计问题上相对现有算法具有更低的采样复杂度。

      论文地址：https://arxiv.org/abs/2212.01571

01 背景与动机

      对于许多问题来说，量子算法可以比经典算法执行得更快，其中一个重要类别是用于线性代数问题的量子算法。近些年，Gilyén, Low, Su 和 Wiebe[1]提出了一种量子矩阵运算框架：量子奇异值变换（Quantum singular value transformation, QSVT），并被广泛应用在线性代数相关的问题中。

      在本文中，我们研究了统计学、理论计算机科学和机器学习中的一个基本问题：统计性质估计，其目的是利用最少的独立样本估计概率分布的属性。一方面，统计属性如熵、散度等，刻画了随机性的一些关键度量。另一方面，相关理论工具在性质测试（property testing）、统计学习等领域中正在迅速发展。在统计性质中，最基本的一个是香农熵，对于[n]上的离散分布\mathbf{p}=(p_{i})_{i=1}^{n}，它被定义为

      香农熵的一个自然推广是Rényi熵，\alpha-Rényi熵被定义为

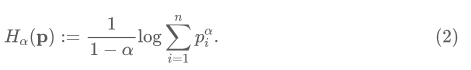
      我们记对数中的幂和为P_\alpha(\mathbf{p})，即P_\alpha(\mathbf{p}) := \sum_{i=1}^n p_i^\alpha。当\alpha\to 1时，Rényi熵趋近于香农熵，即\lim_{\alpha\to 1} H_{\alpha}(\mathbf{p})=H(\mathbf{p})。

02 贡 献

      技术上我们综合了 QSVT，量子退火，和可变时间振幅估计算法[4]，提出了一套完整的估计离散概率分布统计性质的量子算法框架。

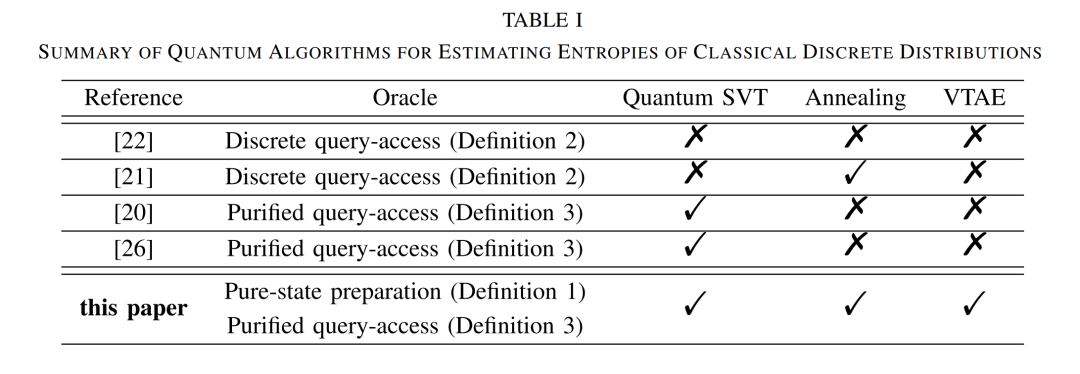
      我们应用该框架在Rényi熵估计问题上，改进了现有量子算法的采样复杂度。图1是本文算法复杂度和之前算法的比较。

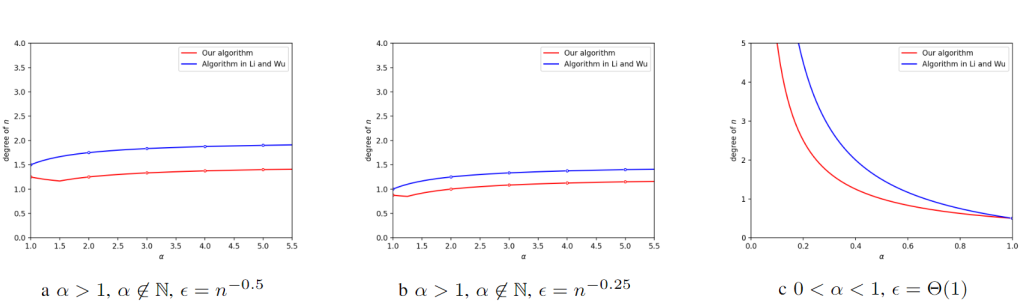
      接下来我们将简要介绍文中技术部分。

      QSVT 与量子退火：

      此前已有一些工作研究估计统计性质的量子算法。Gilyén 和 Li[2]用基于 QSVT 的量子算法估计香农熵，并证明其需要的样本数关于分布维数的依赖项相对于经典算法有根号加速。Gilyén 和 Li[2]通过把待估计的概率分布编码在对角阵中，利用 QSVT 对该矩阵的每一个对角项做近似于x\to\log(x)的变换，最后用振幅估计算法得到香农熵的一个估计。对于Rényi熵估计，Li 和 Wu[3]用一种混合了经典采样和量子均值估计的算法实现了样本数的量子加速。基于香农熵和Rényi熵的相似性，似乎能够仿照 Gilyén 和 Li[2]利用 QSVT 设计使用更少样本估计Rényi熵的量子算法。但是直接仿照 Gilyén 和 Li[2]得到的算法的效果很差，原因是我们只能通过估计P_\alpha(\mathbf{p})到相对误差\epsilon来间接估计H_\alpha(\mathbf{p})到加性误差O(\epsilon)，对于\alpha > 1，P_\alpha(\mathbf{p})可能会非常小，这导致最后的振幅估计算法开销过大。

      受到 Li 和 Wu[3]中的退火过程启发，注意到对于\alpha'=\alpha/(1+1/\log(n))，P_{\alpha'}(\mathbf{p})=\Theta(P_{\alpha}(\mathbf{p}))，因此如果有P_{\alpha'}(\mathbf{p})的粗略估计，我们就能得到P_{\alpha}(\mathbf{p})的粗略估计，从而通过调整 QSVT 的参数预先放大被估计统计量，降低振幅估计的开销。而对于P_{\alpha'}(\mathbf{p})的粗略估计，我们取\alpha''=\alpha'/(1+1/\log(n))，并递归式地估计P_{\alpha''}(\mathbf{p})从而得到P_{\alpha'}(\mathbf{p})的粗略估计，只需对数k=\Theta(\log(n)\log(\alpha))轮递归后，\alpha^{(k)} \approx 1，这时P_{\alpha^{(k)}}(\mathbf{p})的取值范围很小，可以直接被高效估计。这个递归过程类似退火算法，所以下称其为量子退火框架。

      对于基于 QSVT 的估计某统计量的量子算法，因被估计量过小导致估计其到一定相对误差需要开销过大的现象普遍存在。如果能找到一族缓慢变化的函数，使得初始函数为被估计函数，终止函数为可被高效估计的函数，那么我们就可以通过量子退火来提前放大待估计函数，从而避免估计量过小的问题。

      可变时间振幅估计与多项式近似：

      QSVT 能实现的变换只有多项式，并且复杂度和多项式度数线性相关。应用中我们需要的往往是非多项式变换，这就需要构造其多项式近似，并分析其带来的误差。以Rényi熵H_{\alpha}(\mathbf{p}),\alpha >1为例，我们需要构造的是幂函数g(x)=x^{\alpha-1}的多项式近似。对无理数\alpha，g(x)在0点的高阶导数发散，无法构造度数为O(\log(1/\epsilon))的多项式使其在包含0点的定义域内近似误差小于\epsilon。但如果只要求多项式在(-1,-\delta)\cup(\delta,1)上近似g(x)，那么近似多项式的度数是能到O(1/\delta \log(1/\epsilon))的。

      我们在此构造的基础上进一步缩小了多项式近似相关的开销。具体来说，我们构造了度数为O(1/\delta \log(1/\epsilon)) 的多项式，满足在(-1,-\delta)\cup(\delta,1)上近似等于g(x)，同时在 [-\delta,\delta]上的增长被控制，这就减小了 QSVT 的带来的总误差。

      同时注意到，多项式度数主要依赖近似的范围\delta，如果已知p_{i}的取值区间，我们可以设置\delta为该区间的下界来最小化开销。对于一般的分布\mathbf{p}=(p_{i})_{i}，我们首先利用相位估计将分布中的概率按大小分组，然后在可变时间量子算法框架（variable-time quantum algorithm）中对不同区间中的概率p_{i}根据该区间下界作用不同的多项式近似 QSVT，并利用可变时间振幅估计算法[4]（variable-time amplitude estimation）估计最后的统计量从而降低开销。

参考文献

[1] Gilyén, András, et al. "Quantum singular value transformation and beyond: exponential improvements for quantum matrix arithmetics." STOC 2019: 193-204.
[2] Gilyén, András, and Tongyang Li. "Distributional Property Testing in a Quantum World." ITCS 2020: 25:1-25:19.

[3] Li, Tongyang, and Xiaodi Wu. "Quantum query complexity of entropy estimation." IEEE Transactions on Information Theory 65.5 (2018): 2899-2921.
[4] Ambainis, Andris. "Variable time amplitude amplification and quantum algorithms for linear algebra problems." STACS 2012: 636-647.