本文是对发表于 NeurIPS 2023 论文 GenPose: Generative Category-level Object Pose Estimation via Diffusion Models 的解读。该论文由北京大学董豪超平面实验室完成，共同一作为计算机学院博士生张继耀、吴铭东。类别级 6D 物体位姿估计是一个基础且重要的问题，在机器人、虚拟现实和增强现实等领域应用广泛。本文提出了一种类别级 6D 物体位姿估计新范式，取得了新的 SOTA 结果。

 

　　*以下内容首发于机器之心。

 

　　论文链接：https://arxiv.org/abs/2306.10531

　　项目视频：https://www.bilibili.com/video/BV1Eg4y1Z7x2/

 

　　6D 物体位姿估计作为计算机视觉领域的一个重要任务，在机器人、虚拟现实和增强现实等领域有众多应用。尽管实例级别的物体位姿估计已经取得了显著进展，但它需要事先了解物体的特性，因此无法轻松适用于新的物体，这限制了其实际应用。为了解决这一问题，近年来，越来越多的研究工作集中在类别级别的物体位姿估计上。类别级别的位姿估计要求算法不依赖于物体的 CAD 模型，能够直接应用到与训练数据中相同类别的新物体。

 

　　目前，主流的类别级别 6D 物体位姿估计方法可以分为两大类：一是直接回归的端到端方法，二是基于物体类别先验的两阶段方法。然而，这些方法都将该问题建模为回归任务，因此在处理对称物体和部分可见物体时，需要特殊的设计来应对多解问题。

 

　　为了克服这些挑战，本文提出了一种全新的类别级 6D 物体位姿估计范式，将该问题重新定义为条件分布建模问题，从而实现了最新的最优性能。

　　

01 类别级 6D 物体姿态估计中的多解问题

 

　　在类别级 6D 物体姿态估计中，多解问题指的是在同一观测条件下，可能存在多个合理的位姿估计。这种情况主要源于两个方面，如图1所示：对称物体和部分观测。对于对称物体，例如球形或圆柱形的物体，在不同方向上的观测可能会完全相同，因此从理论上讲，它们有无限多个可能的位姿真值。同时，单一视角无法获取到完整的物体观测，例如马克杯，在没有观察到杯柄的情况下，也存在无限多个可能的位姿真值。

图1. 多解问题的来源：对称物体和部分观测

　　

02 方法介绍

 

　　那么如何应对上述多解问题呢？作者把该问题看作条件分布建模问题，提出了一种名为 GenPose 的方法，利用扩散模型来估计物体位姿的条件分布。该方法首先使用基于分数的扩散模型生成物体位姿的候选项。然后通过两步对候选项进行聚合：首先，通过似然估计筛选掉异常值，接着通过平均池化对剩余候选位姿进行聚合。为了避免在估计似然时需要繁琐的积分计算，研究作者还引入了一种基于能量的扩散模型的训练方法，以实现端到端的似然估计。

图2. GenPose 框架结构

　　

基于分数的扩散模型用于物体姿态候选的生成

 

　　这一步骤旨在解决多解问题，那么如何建模物体位姿的条件概率分布呢？作者采用了基于分数的扩散模型，利用 VE SDE（Variational Eulerian Stochastic Differential Equation）构建了一个连续的扩散过程。在模型的训练过程中，其目标是估计扰动条件姿态分布的分数函数，并最终通过 Probability Flow ODE（Ordinary Differential Equation）从条件分布中采样物体姿态的候选项。

 

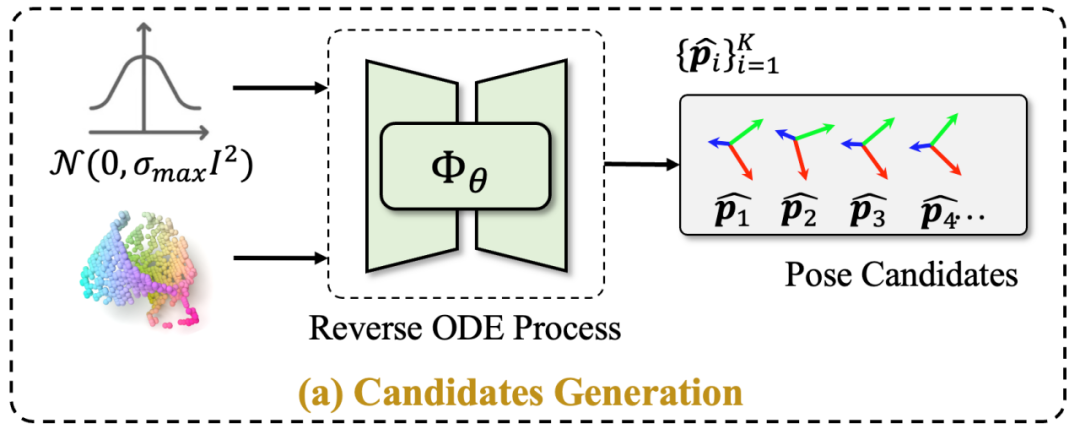
图3. 基于分数的扩散模型生成物体姿态候选

 

基于能量的扩散模型用于物体姿态候选的聚合

 

　　从训练好的条件分布可以采样出无限个物体位姿候选，如果从候选中得到一个最终的物体位姿呢？最直接的方式是随机采样，但是这种方法无法保证预测的稳定性。是否可以通过平均池化来聚合候选项呢？然而这种聚合方式未考虑候选的质量，容易受到离群值的影响。作者认为可以通过似然估计的方式把候选的质量作为聚合的参考。具体来说，根据似然估计结果对物体姿态候选进行排序，过滤掉似然估计较低离群候选后对剩余候选进行平均池化，就可以得到聚合后的姿态估计结果。但是，扩散模型进行似然估计需要繁琐的积分计算，这严重影响了推理速度，及其限制其实际应用。为了解决这个问题，作者提出训练一个基于能量的扩散模型，直接用于进行端到端的似然估计，实现候选的快速聚合。

 

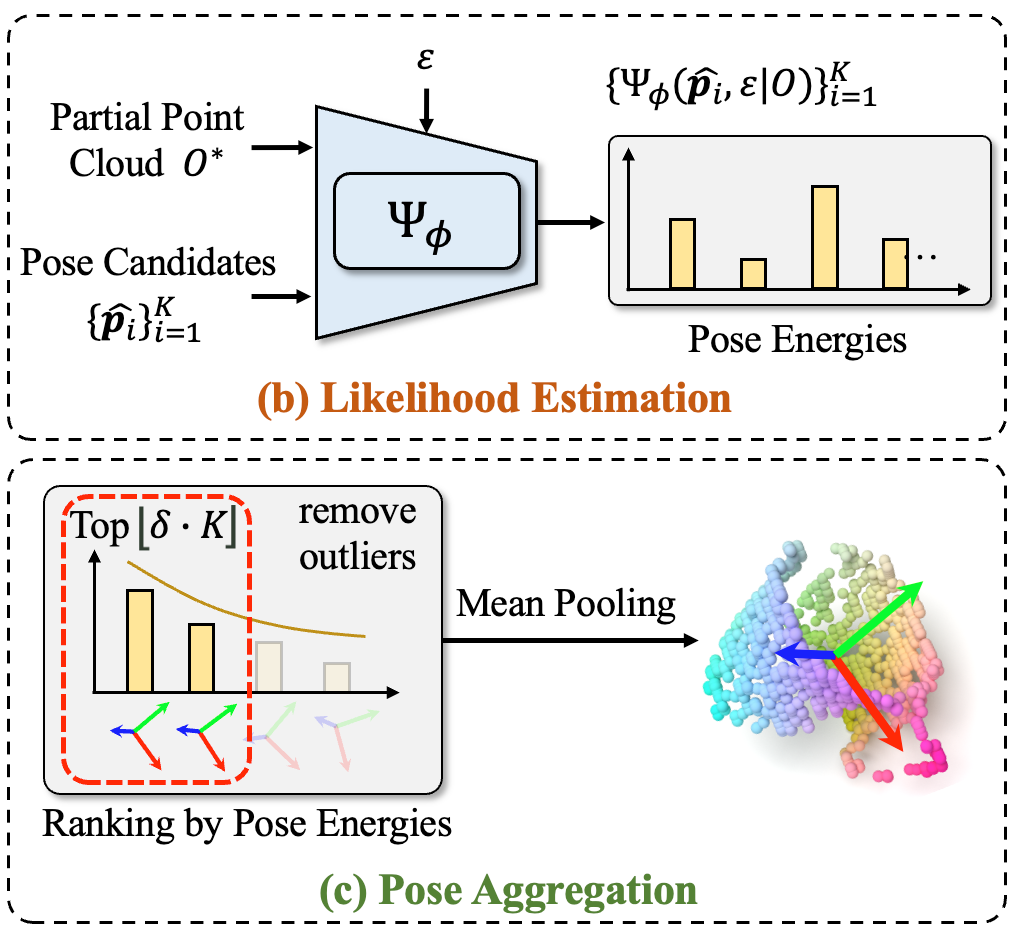
图4. 基于能量的扩散模型用于似然估计与物体姿态候选聚合

　　

03 实验与结果

 

　　作者在 REAL275 数据集上对 GenPose 性能进行了验证，可以看出 GenPose 在各项指标上都大幅优于之前的方法，即使是与使用更多模态信息的方法进行对比，GenPose 依然有很大的领先优势，表1展示了作者提出的生成式物体姿态估计范式的优势。图5是可视化的结果。

 

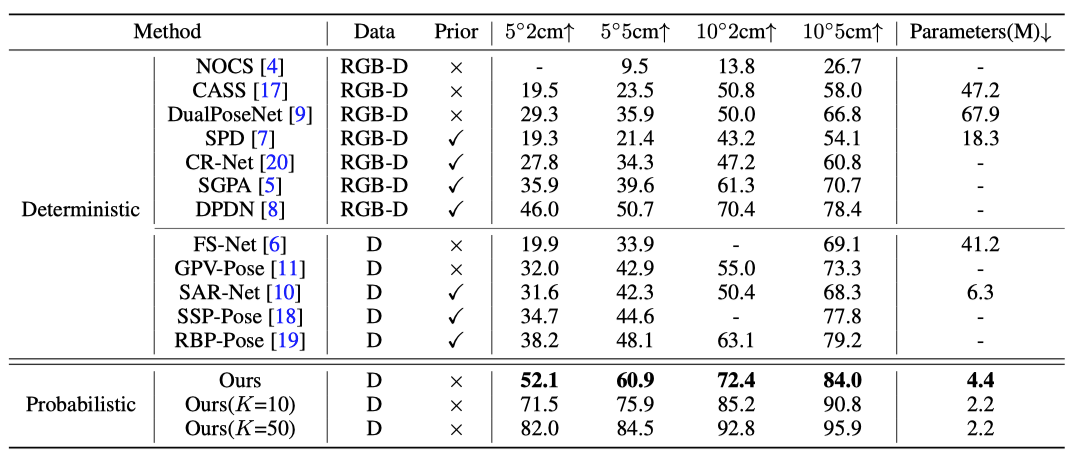
表1. 与其他方法的对比

　　

图5. 不同方法的预测可视化效果

 

　　作者还研究了使用不同的聚合方法（随机采样，随机排序后聚合、基于能量排序后聚合、GT 排序后聚合）的影响。可以看出使用能量模型进行排序明显优于随机抽样方法。可以看出作者提出的基于能量的扩散模型对物体姿态候选进行聚合的方法明显由于随机采样的方法和随机排序后平均池化的方法。

 

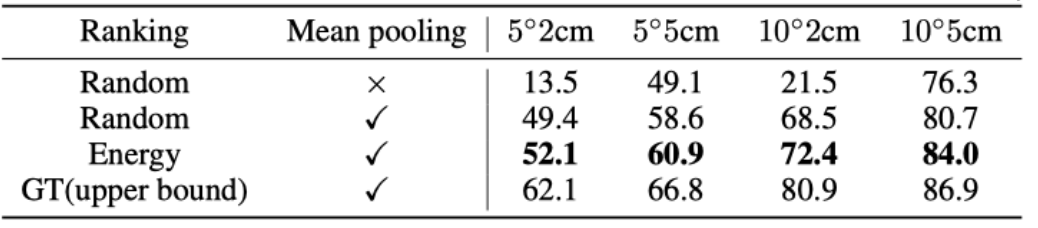
表2. 不同聚合方式的对比

 

　　为了更好地分析能量模型的影响，作者进一步研究了估计的位姿误差与预测的能量之间的相关性。如图6所示，预测的位姿误差和能量之间存在一般的负相关关系。能量模型在识别误差较大的姿态时表现较好，而在识别误差较小的姿态时表现较差，这解释了为什么预测的能量被用来去除离群点，而非直接选出能量最大的候选。

 

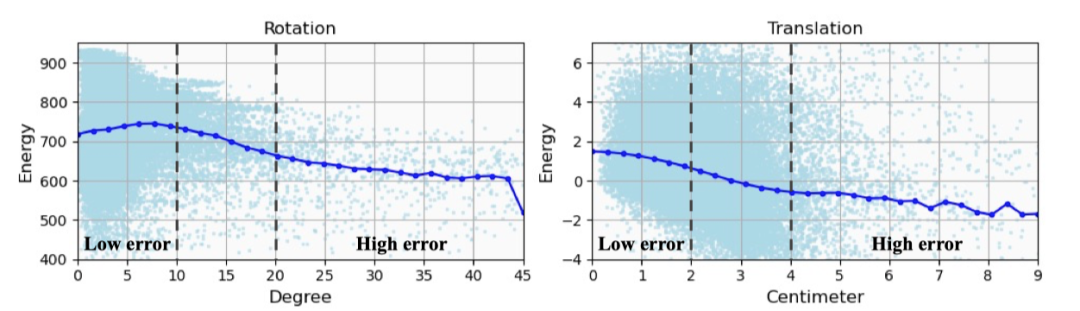
图6. 能量与预测误差相关性分析

 

　　作者还展示了该方法跨类别泛化的能力，该方法不依赖类别先验，在跨类别的泛化上的表现也显著优于之前的方法。

 

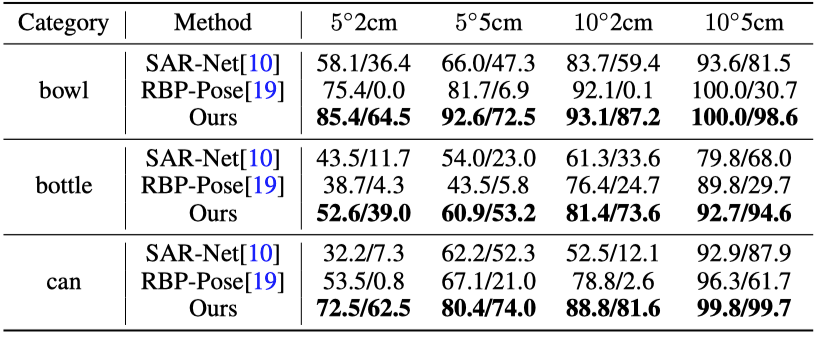
表3. 跨类别泛化效果

‘/’ 左边表示训练数据集包含测试类时的性能，‘/’ 右边表示把训练时把测试的类别移除时候的性能。

 

　　同时，由于扩散模型的闭环生成过程，文章中的单帧姿态估计框架还可以直接用于 6D 物体姿态跟踪任务，没有任何特殊的设计，该方法在多项指标中优于最先进的 6D 物体姿态跟踪方法，结果如表4所示。

 

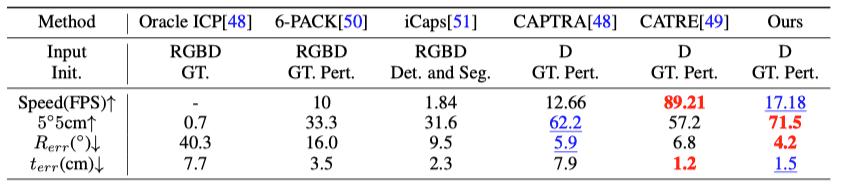
表4. 类别级 6D 物体姿态追踪性能对比

　　

04 总结与展望

 

　　这项工作提出了一个类别级 6D 物体位姿估计新范式，训练过程无需针对对称物体和部分观测带来的多解问题做任何特殊设计，取得了新的 SOTA 性能。未来的工作会利用扩散模型的最新进展来加速推理过程，并考虑结合强化学习来实现主动式 6D 物体位姿估计。