本文是对发表于机器学习领域顶级会议 NeurIPS 2023 的论文 Causal Discovery from Subsampled Time Series with Proxy Variable 的解读。该论文由北京大学王亦洲课题组和复旦大学孙鑫伟助理教授合作完成，第一作者为北京大学计算机学院博士生刘鸣洲。本文提出了一种基于代理变量（Proxy Variables）的时序因果发现理论，首次实现了非参意义下的因果图识别性保证。本文根据该理论设计了一种基于条件独立性测试的因果发现算法，在仿真实验和阿尔茨海默疾病分析中取得了优秀表现。

 

　　论文链接：https://arxiv.org/abs/2305.05276

　　开源代码：https://github.com/lmz123321/proxy_causal_discovery

 

01 方法概览

 

　　时间系统的因果分析是人工智能和科学计算中的重要问题。对这类系统而言，一个常见的问题是数据采样的时间分辨率不足（Subsampling Problem）。例如，在视频分析中每间隔10-30帧才有一帧为关键帧，在疾病病因分析中每间隔6-12个月才有一次随访记录。在这些问题中，采样速率都远远低于因果过程发生的速率。

 

　　采样速率的不足会对因果结构的识别造成严重障碍。这是由于当前的因果理论主要建立在对系统具备完全观测（Causal Sufficiency Condition）的基础上。当系统中存在未观测变量时，所引入的偏移会导致因果发现算法失效。例如，未观测变量M引入的中介偏移，会导致算法无法区分直接因果效应（A→B）和间接因果效应（A→M→B）。

 

　　为解决这一问题，许多工作尝试建立采样率不足情况下的时序因果识别理论。然而，这些工作或受限于线性模型[1,2,3]，或无法实现完全的可识别性[4,5,6]，制约了它们在实际问题中的应用。

 

　　为此，本文提出一种基于代理变量的时序因果发现理论。该理论的核心观察在于，在时间序列中，每个未观测变量都存在一个可观测的后代（即该变量在未来某个可观测时刻的测量）。因此，我们可以利用这一可观测后代作为未观测变量的代理变量（Proxy Variable）[7,8]，对未观测变量引入的偏移进行调整。

 

　　具体来说，本文首先利用极大祖先图（Maximal Ancestral Graph, MAG）表示观测分布中提现的祖先关系（包含直接因果关系和间接因果关系）；进而，本文利用代理变量区分直接因果关系和间接因果关系，实现了因果结构的可识别性。值得注意的是，本文提出的因果识别理论不需要任何的参数化假设，可以恢复完整的因果结构，具有广泛的应用价值。

 

02 背景介绍

 

　　时间序列模型

　　考虑一个含有d个随机变量的离散时间序列\mathbf{X}(t):=[X_1(t),...,X_d(t)],t=1,2,...,T。我们假设X(t)由一个一阶结构向量自回归（First-order Structural Vector Autoregression, SVAR）过程生成：

X_i(t)=f_i({\mathbf{PA}}_i(t-1),N_i)

 

　　其中f_i表示结构方程，{\mathbf{PA}}_i表示X_i的因果父节点，N_i表示外源噪声。

 

　　这一模型包含了两个常见的假设，即原因优先假设（因变量{\mathbf{PA}}_i(t-1)发生在果变量X_i(t)之前）和因果时间不变假设（结构方程f_i所表示的因果关系不随时间改变）。此外，我们还假设该模型只能每间隔k个时间步被观察一次。

 

　　因果图术语

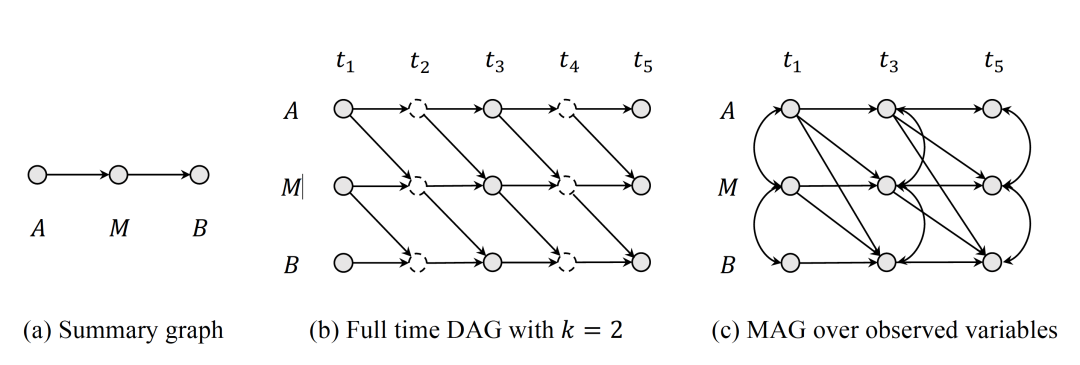
图-1. 因果图术语，图中实线表示可观测变量，虚线表示不可观测变量。(a) 总结图（Summary Graph）；(b) 采样率k=2的全时间有向无环图（Full Time DAG）；(c) 可观测变量上的极大祖先图（MAG）

 

　　时序模型中蕴含的因果关系，可以用各种因果图来表示（图-1）。我们首先介绍全时间有向无环图（Full Time Directed Acyclic Graph, DAG），它描述了系统的完整动态信息。

 

　　定义-1：（全时间有向无环图）令G:=(V, E)为 SVAR 模型对应的全时间有向无环图，其结点集为\mathbf{V}:={{\mathbf{X}(t)}}_{t=1}^T，边集E包含X_i(t-1)→ X_j(t)当且仅当X_i\in{\mathbf{PA}}_j 。

 

　　我们假设全时间有向无环图对联合分布\mathbb{P}(\mathbf{X}(1),...,\mathbf{X}(T))满足以下的马尔科夫和忠实性（Markovian and faithfulness）假设。

 

　　假设-1：（马尔科夫和忠实性）对于不相交的节点集合A,B,Z，我们有\mathbf{A}\bot\mathbf{B}|\mathbf{Z}当且仅当\mathbf{A}\bot_G\mathbf{B}|\mathbf{Z}，其中\bot_G表示图G中的d-分离（d-separation）。

 

　　在实际问题中，通常只需要了解各个时间序列间的因果关系，对于时间步不必进行精确的描述。因此，我们常使用因果总结图（Summary Graph）[9]：

 

　　定义-2：（总结图）令G:=(V, E)为时序模型对应的总结图，其结点集为V:=X，边集E包含X_i→ X_j 当且仅当 X_i\in{\mathbf{PA}}_j。

 

　　本文的目标就是从观测数据中恢复因果总结图。为了实现这一目标，我们还需要一种因果图来描述观测变量之间的（边缘）因果关系，进而将观测分布与总结图联系在一起。具体来说，我们考虑极大祖先图（MAG）[10]：

 

　　定义-3：（极大祖先图）对随机变量集合\mathbf{V}:={{\mathbf{X}(t)}}_{t=1}^T，令\mathbf{O}:={\mathbf{X}(1),\mathbf{X}(t+k),\mathbf{X}(t+2k),...}为可观测子集，\mathbf{L}:=\mathbf{V}\\mathbf{O}为不可观测子集。令An(A)表示节点A的祖先。给定V上的任意一个全时间有向无环图G，则其对应的O上的极大祖先图M_G中，两个节点A,B相邻当且仅当G中存在一条相对于L的诱导路径（Inducing Path），A,B间边的指向为：

1. M_G中含A→B，若G中A∈An(B) ；
2. M_G中含A←B，若G中B∈An(A) ；
3. M_G中含A\leftrightarrowB，若G中B∉An(A) 且A∉An(B)。

　　

　　代理变量

　　近期的研究工作发现[8]，未观测变量M的代理变量能用于区分直接因果效应（A→B）和间接因果效应（ A→M→B）：

 

　　定理-1：（[8]，定理-4.8）假设A,B间存在一个未观测的中介变量M，且M有一个代理变量M^\prime满足A\bot_GM^\prime|M，则可以通过检测pr(b|a)~pr(m^\prime|a)之间是否满足线性关系来区分A→B和A→M→B。若线性关系不存在，则为A→B，否则为A→M→B。

 

　　为了保证代理变量存在，我们还需要以下的自原因（Self Causation）假设。

 

　　假设-2：（自原因）在 SVAR 模型中，对任何的i，均有X_i\in{\mathbf{PA}}_i。

 

03 因果识别理论

 

　　我们首先证明了极大祖先图的可识别性。

 

　　命题-1：（极大祖先图的可识别性）在 SVAR 模型以及假设-1,2下，O上的极大祖先图是可识别的。具体来说，它的骨架（Skeleton）和边的指向可以从分布\mathbb{P}(\mathbf{O}) 中唯一的确定出来。

 

　　进而，我们在命题-2中研究了极大祖先图与总结图的关系。

 

　　命题-2：（从极大祖先图到总结图）若在极大祖先图中存在A(t)→B(t+k)和A(t+k)\leftrightarrowB(t+k)，则在总结图中存在：

1. A→B，或
2. 一条从A到B的长度小于等于k-2的有向路径，或
3. 一条从A到B的长度等于k-1的有向路径和一个长度为(r≤k-2, q≤k-2)的混淆结构。

 

　　命题-2说明极大祖先图能反应因果总结图的大部分信息。我们只需区分直接因果效应（A→B）和间接因果效应（A到B有一条有向路径），就能识别出因果总结图。依据这一思想，我们利用代理变量证明了因果总结图的可识别性。

 

　　定理-2：在 SVAR 模型以及假设-1,2下，因果总结图是可识别的。具体而言，

1. 在因果总结图中存在A→B当且仅当在极大祖先图中存在A(t)→B(t+k)和A(t+k)\leftrightarrowB(t+k)，且集合M(t+1)∪S(t)不足以d-分离A(t), B(t+k)。
2. 条件“集合M(t+1)∪S(t)不足以d-分离A(t), B(t+k) ”可以利用定理-1，通过未观测变量M(t+1)的代理变量M(t+k) 测试。

 

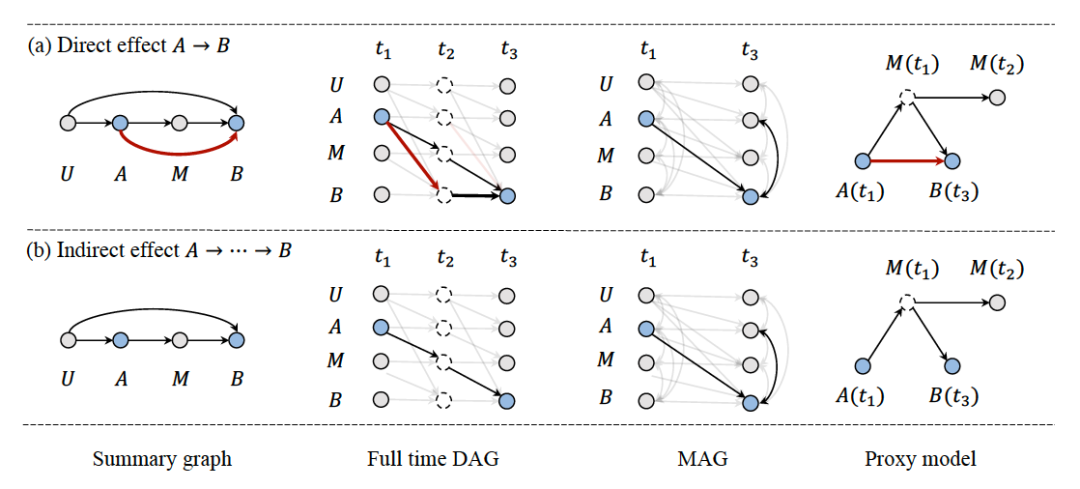
图-2. 示例：利用代理变量区分直接因果效应（A→B）和间接因果效应（A→...→B），进而识别因果总结图

 

04 因果发现算法

 

　　根据上述因果识别理论，本文提出了一种高效的因果发现算法（算法-1）。该算法首先恢复出可观测变量上的极大祖先图；其次，利用极大祖先图和定理-2中的必要条件建立因果总结图中的潜在边；最后，利用代理变量识别并删去表示间接因果关系的潜在边，得到完整的总结图。

 

算法-1. 本文提出的因果发现算法

 

05 实验结果

 

　　我们首先在仿真数据上进行了实验（图-3）。由于具备可识别性理论保证，本文提出的算法表现远超基线方法。

 

图-3. 仿真实验效果对比

 

　　我们还恢复了阿尔茨海默疾病在九十个重要脑区上的因果图（图-4），该因果图与许多临床经验相印证[11]，这进一步验证了本文提出的因果发现算法的有效性。

 

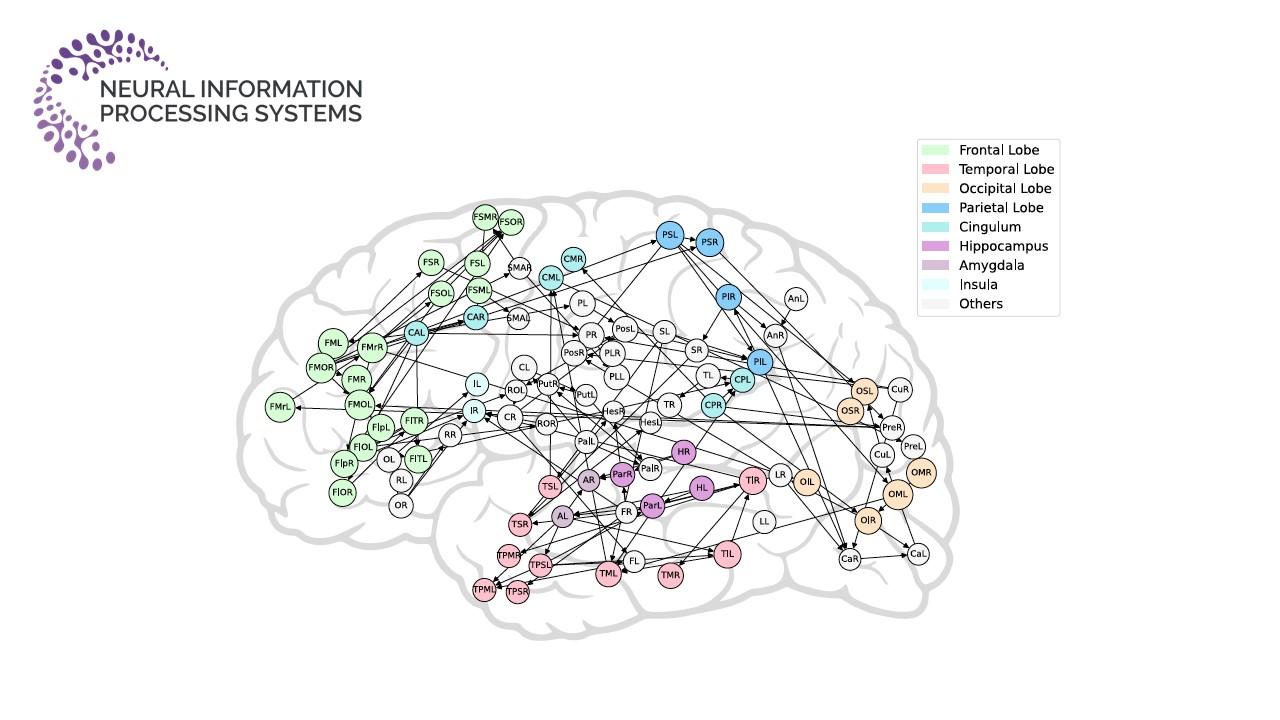
图-4. 阿尔茨海默疾病因果图

 

参考文献

[1] M Gong et al. Discovering temporal causal relations from subsampled data. ICML 2015.

[2] M. Gong et al. Causal discovery from temporally aggregated time series. UAI 2017.

[3] A. Tan et al. Identifiability and estimation of structural vector autoregressive models for subsampled and mixed-frequency time series. Biometrika 2019.

[4] S. Plis et al. Rate-agnostic (causal) structure learning. NeurIPS 2015.

[5] A. Hyttinen et al. Causal discovery from subsampled time series data by constraint optimization. Conference on Probabilistic Graphical Models 2016.

[6] D. Malinsky et al. Causal structure learning from multivariate time series in settings with unmeasured confounding. ACM SIGKDD 2018.

[7] M. Kuroki et al. Measurement bias and effect restoration in causal inference. Biometrika 2014.

[8] Mingzhou Liu et al. Causal discovery with unobserved variables: a proxy variable approach. arXiv preprint arXiv:2305.05281, 2023.

[9] C. Gong et al. Causal discovery from temporal data: An overview and new perspectives. arXiv preprint arXiv:2303.10112, 2023.

[10] J. Zhang. On the completeness of orientation rules for causal discovery in the presence of latent confounders and selection bias. Artificial Intelligence 2008.

[11] G. S Bloom. Amyloid-β and tau: the trigger and bullet in alzheimer disease pathogenesis. JAMA neurology, 71(4):505–508, 2014.