2023年9月18日、20日以及22日，香港大学的黄志毅副教授访问北京大学前沿计算研究中心，在静园五院连作三场关于 Data-driven Auction Design 的讲座，讲座从模型定义一直到理论最新进展，逐步介绍了数据驱动的拍卖机制设计领域的一系列研究成果。这次系列讲座由中心助理教授姜少峰老师主持。

　　

　　该系列讲座受到了北京大学海外学者讲学计划支持。

　　

　　
黄志毅老师报告现场(报告视频：
1. https://www.bilibili.com/video/BV1D84y1S7G1/
2. https://www.bilibili.com/video/BV1xp4y1F72g/
3. https://www.bilibili.com/video/BV1FV411w7bu/)

　　

讲座1：基础模型与理论技术

　　

　　在第一场讲座中，黄老师首先介绍了基础的拍卖模型。一个基本的拍卖形式是将一个物品拍卖给若干买家，其中第i个买家会对该物品有一个随机的估价v_{i}，并且报价b_{i}。卖家需要根据所有买家的报价\left\{ b_{i} \right\}_{i}来确定物品的分配方式\left\{ x_{i} \right\}_{i}（满足 \Sigma_{i}x_{i}=1）以及收费方式\left\{ p_{i} \right\}_{i}。这里，p_{i}表示买家i需要支付的费用，x_{i} 为获得物品的概率。

　　

　　拍卖机制设计的目标是设计一种从买家的报价\left\{ b_{i} \right\}_{i}到物品的分配方式\left\{ x_{i} \right\}_{i}以及收费方式\left\{ p_{i} \right\}_{i} 的映射，以最大化卖家的期望收益。

　　

　　

　　一般情况下，我们会希望所设计的拍卖机制是占优策略激励相容（Dominant-Strategy Incentive Compatibility，简称DSIC）以及个体理性（Individually Rational，简称IR）的。简而言之，这意味着所有买家在该拍卖机制下都倾向于诚实地报出他们的真实估价，即b_{i}=v_{i}。

　　

　　

　　在之后的讲座中，黄老师重点介绍了单买家情形下的结果。当假设拍卖中只存在一个潜在买家时，DSIC 和 IR 的拍卖等同于一个定价问题。也就是说，需要确定一个价格p，当买家的估价v大于p时，他会支付价格p来购买该物品。因此，卖家的期望收益为p\cdot q(p)，其中 q(p)为买家的估价不低于p的概率。

　　

　　在数据驱动的最优定价问题中，假设买家的估价服从[0,1]上的某一分布D。我们没有关于这个分布的任何先验信息，但我们可以通过采样样本来获取信息。因此，我们追求的目标是确定从分布D中采样多少独立同分布的样本（即采样复杂度），能获得足够多的信息，以实现（近似）最优的定价策略。

　　

　　

　　针对采样复杂性的上界和下界，黄老师分别介绍了所需的理论工具和证明思路。考虑采样复杂度的上界时，一个经典的“三步走”证明框架是：首先考虑了对单个p，需要多少采样才能以1-δ 的概率对q(p)进行误差不超过\epsilon的估计。这一步骤可以运用一些基本的集中不等式得出\widetilde{O}\left(\epsilon^{-2} \log \frac{1}{\delta}\right)的采样复杂度。随后，我们计算价格空间[0,1]的一个覆盖（covering）的大小。简单来说，一个覆盖是价格空间的一个子集，只要能准确估计覆盖中的价格的q(p)，就可以估计价格空间中所有价格的q(p)。利用离散化方法可以证明存在一个大小为\epsilon^{-1}的覆盖。最后借助联合界不等式（union bound），我们可以得到 \widetilde{O}\left(\epsilon^{-2} \log \frac{1}{\epsilon\delta}\right)的采样复杂度。

　　

　　

　　而对于采样复杂度的下界，黄老师介绍一种名为 Le Cam's method 的方法，将一个区分两个分布的问题归约到定价问题。最终可以得到一个与上界匹配的\Omega (\epsilon^{-2})的下界。

 

　　最后，黄老师总结了将这一证明框架应用于不同分布时所获得的结果，指出这一技术能够获得几乎紧的理论上下界的结果。

　　

　　

讲座2：统计学习理论方法的研究进展

　　

　　在第二场讲座中，黄老师讲解了在有n≥1个买家情形下的拍卖机制设计。此时，我们需要利用迈尔森理论（Myerson's theory）。该理论将 DSIC 和 IR 的拍卖机制设计问题转化为计算一个最大化虚拟社会福利（virtual welfare）的单调分配函数。该问题可以被视为一个学习问题，即，从所有可行的分配函数构成假设空间（hypothesis space）中学习到一个最大化虚拟社会福利的假设。

　　

　　

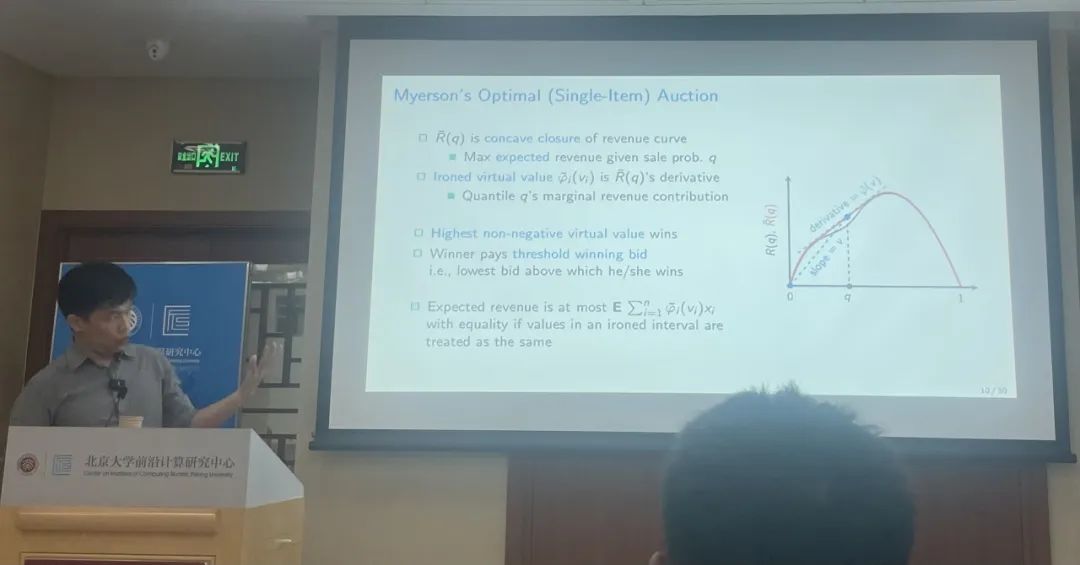
　　因此，利用统计学习理论的方法来解决采样复杂度问题是一种思路。第二场讲座的第一部分综述了这一思路下的大部分成果。这些成果采用了与单买家情形相同的“三步走”证明框架，而在第二步中，我们需要计算假设空间的覆盖的大小。统计学习理论的思路是通过刻画和分析假设空间的“维度”，例如 VC 维度、伪维度（pseudo dimension）等，来估计覆盖的大小。最终基于统计学习理论的思路可以获得采样复杂度为\tilde {O}(n\epsilon^{-3})。

　　

　　在第二场讲座的第二部分中，黄老师讲解了一种更为直接的证明思路。我们发现任何一个分配函数都可以由n个函数表达，且每个函数是[0,1]到(-\infty,1]的映射。因此，通过对定义域和值域进行适当的离散化，我们可以得到一个大小为\epsilon^{-O(n/\epsilon)}的覆盖大小，从而可以得到与统计学习方法几乎一致的采样复杂度。

　　

　　

　　关于采样复杂度的下界，黄老师说明了 Le Cam's method 不足以得到匹配的下界。因此，他介绍了一种更为精细的方法，即 Assouad's method，成功地推导出了Ω(n\epsilon^{-2})的采样复杂度下界。

　　

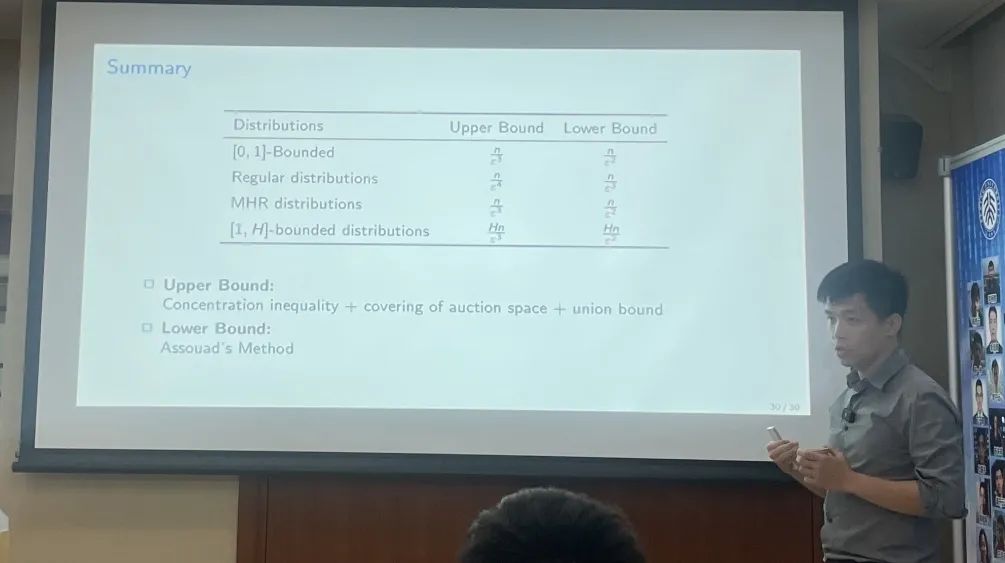
　　最后，黄老师总结了在不同分布下得到的采样复杂度的上下界。值得注意的是，在所有分布中，采样复杂度的上下界之间在\epsilon的指数上都相差一阶。

　　

　　

讲座3：乘积分布的可学习性与强收益单调性

　　

　　在第三场讲座中，黄老师首先比较了学习卖家收益函数与学习买家估价分布两种解决问题的思路，并说明了两者在单买家情形下其实是等价的。而对于多买家的拍卖机制设计，情况会略微复杂。

　　

　　

　　因此，黄老师首先介绍了一种新的概率分布的距离度量，即 Hellinger 距离，并证明当两个分布的 Hellinger 距离足够接近时，计算得到的迈尔森最优拍卖的期望收益之间的差异同样会很小。

　　

　　随后，黄老师给出一个定理，即在分布D的支撑集是有限的且大小为k的前提下，要使在支撑集上定义的经验分布E与真实分布D之间的 Hellinger 距离不超过\epsilon，只需要O(k\epsilon^{-2})个采样样本即可。利用这个结论，我们可以对n个买家的估价分布进行离散化，使其支撑集有限化，即可直接得到与第二场讲座中一致的O(n\epsilon^{-3})的采样复杂度上界。

　　

　　

　　为了得到更紧的上界，黄老师引入一种称为强收益单调性（Strong Revenue Monotonicity）的概念。结合估计分布的方法，我们可以得到与下界匹配的O(n\epsilon^{-2})的采样复杂性。该算法的关键在于，我们将理论误差加到经验分布E上，得到新分布\bar{E}，然后将\bar{E}上的迈尔森最优拍卖M_{\bar{E}}作为估计输出。在分析中，我们用类似的方法构造一个新的分布\bar{D}，使得分布\bar{E}被“夹在”D和\bar{D}之间。通过证明一种强收益单调性的性质，我们可以得到M_{\bar{E}}在D上的收入不低于\bar{D}上的最优拍卖的收益。最后，通过证明采样数为O(n\epsilon^{-2})（忽略对数因子）时，D和\bar{D}的最优拍卖的收益相差不超过\epsilon，我们最终证明了M_{\bar{E}}是一个近似最优的拍卖机制。

　　

　　

　　讲座的最后，黄老师讨论了一些相关的开放问题，例如多参数买家的拍卖问题（multi-parameter auctions）、随机模型下的序贯决策问题（sequential decision-making in stochastic models）等。

　　

　　
合影留念