本文是对发表于机器学习领域顶级会议 ICML 2023 的论文 Which Invariance Should We Transfer? A Causal Minimax Approach 的解读。该论文由北京大学王亦洲课题组与复旦大学孙鑫伟助理教授合作完成，第一作者为北京大学计算机学院博士生刘鸣洲。

　　

　　本文提出了一种基于主动干预（Intervention）的分布外泛化算法。该算法具有完备的最优性保证，并且可以通过等价类搜索的方式大幅降低计算复杂度。在阿尔茨海默疾病诊断中，该算法的泛化性能超越已有方法15%，计算代价降低99%以上，显示出强大的威力。

　　

　　论文链接：https://proceedings.mlr.press/v202/liu23bc/liu23bc.pdf

　　项目代码：https://github.com/lmz123321/which_invariance

　　视频介绍：https://youtu.be/5hmyl1hP-6k

　　

01 方法概览

　　

　　当前的机器学习系统普遍依赖于独立同分布假设（Independent Identical Distribution, IID）。当训练环境与部署环境的分布出现偏移时，这些模型的预测将不再可靠，从而可能导致严重后果。为了解决这一问题，研究人员普遍认为可泛化的机器学习系统应具备两个特征，即稳定性（Stability）和鲁棒性（Robustness）。前者是指预测行为对分布偏移的不敏感性，而后者则是描述泛化误差的可控性。

　　

　　为了实现这一目标，已有工作提出挖掘并迁移数据中的不变性（Invariance)，如 Peters Jones 等人提出的 ICP 算法利用目标变量的稳定父节点进行预测。然而，这些方法只能被动利用观测数据中不变性，无法对变化的环境进行主动适应，限制了它们的应用潜力。

　　

　　为此，本文提出一种基于主动干预的分布外泛化方法。该方法首先通过因果发现自动识别系统中的不稳定成分。进而，通过对这些不稳定成分进行干预，得到了一个稳定的干预分布。与被动观测的条件分布相比，该干预分布具有更优的不变性质。最后，本文在干预分布上定义了一族稳定的预测模型，并通过等价类搜索的方式识别出其中最鲁棒者，从而实现了稳定性和鲁棒性的兼优。

　　

02 背景介绍

　　

干预

　　干预是对人类主动行为（Action）的数学抽象。这一概念最早由 Judea Pearl 等人[1]在结构因果模型框架中提出。具体来说，对某个变量X的干预，通常被记作do(X=x)，是指将X从它原有的因果机制中抽离出来，并强行赋予其新的状态x。从因果图上看，对X的干预就是删除所有指向X 的边。

 

　　以开关灯为例，do(开关=开)就表示不管开关的原有状态如何、受何种因素（声音、触摸）的影响，强行打开开关。

　　

分布偏移的因果解释

 

　　根据 Scholkopf 等人[2]提出的稀疏机制偏移理论（Sparse Mechanism Shift Hypothesis），数据分布P^{e}(X,Y)中的分布偏移（e 表示不同的环境），是由于部分变量的因果机制发生变化导致的。

　　

　　这也就是说，只有部分变量的因果机制会随着环境的改变而发生变化，而其余变量的机制则保持稳定。相应的，我们将前者称为不稳定变量（Mutable Variables,X_{M}），它们是数据分布出现偏移的根本原因；后者则称为稳定变量（Stable Variables, X_{S}）。

　　

03 通过干预实现不变性

　　

　　如前文所指出的，不稳定变量的因果机制是数据分布发生偏移的根本原因。因此，对不稳定变量进行干预，删除它们随环境变化的因果机制，就能去除系统中随环境发生偏移的成分，从而得到对不同环境具有不变性的稳定分布。

　　

　　具体来说，本文有以下结论：

　　【命题-1】干预分布

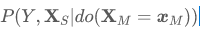
　　对于不同环境e保持不变。

　　

　　值得注意的是，数据中的不稳定变量X_{M}可以由因果发现算法[3]自动识别。因此，上述命题中给出的干预分布是可计算的。

　　

　　基于命题-1，我们推导出一族具备稳定性的预测器，该族中的每一个成员f_{S'}(x)对应稳定变量集合S的一个各个子集S'：

　　

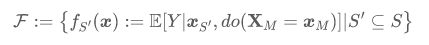
04 最优性理论

　　

　　针对前文介绍的稳定预测器族，一个自然的问题是：该族中的哪一个成员是最鲁棒的？换言之，在所有成员中哪一个预测器的泛化误差最小？

　　

　　在本文中，我们用最差情况风险（Worst-case Risk）- 即所有部署环境中的最差预测误差 - 来衡量预测器的鲁棒性。因此，最鲁棒的预测器f*应该具有以下的极大极小最优性（Minimax Optimum）：

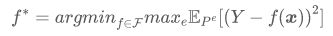
　　为了识别上述最鲁棒预测器，我们提出利用训练环境估计每个预测器的最差情况风险，从而通过比较选出最优者。具体来说，我们设计了一个仿真分布族,

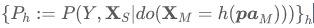
　　其中h是从不稳定变量的父节点PA_{M}到不稳定变量X_{M}的一个映射函数。这一分布族保持了原有分布的稳定成分，同时允许X_{M}基于它们的父节点任意变化，从而可以模拟潜在部署环境中的分布偏移行为。

　　

　　理论分析表明，从该仿真分布族中测得的最差情况风险与实际部署中的最差情况风险完全相同：

　　【定理-1】令

　　

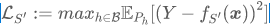
　　为仿真分布族\left\{ P_{h} \right\}_{h}上测得的最坏情况风险，令R_{S'}为实际部署中的最差情况风险，则对于任何S'\subseteqS，均有 L_{S'}=R_{S'}。

　　

05 图等价类

　　

　　根据定理-1，我们需要逐个估计F中各个预测器的最差情况风险，其计算复杂度与稳定变量个数成指数关系。

　　

　　为了降低这一复杂度，我们提出了图等价类的概念。具体来说，我们发现F中的存在许多相互等价的预测器，由相互等价的预测器所构成的集合就是一个等价类。进而，搜索范围可以由F中所有的预测器，减少到F中所有的等价类。同时，我们发现F中所有的等价类均可从其因果图中识别出来，这就为图等价类搜索提供了实现算法。

　　

　　理论分析表明，图等价类可以将搜索复杂度由指数级降低为多项式级。

　　

　　此外，值得注意的是，上述图等价类搜索算法适用于任何因果图模型（如有向无环图 Directed Acyclic Graph DAG，极大祖先图 Maximal Ancestral Graph MAG），因此有广泛的应用价值。

　　

06 实验结论

　　

　　为了验证本文理论的有效性，我们在阿尔兹海默疾病（Alzheimer's Disease, AD）诊断任务上进行了实验。

　　

　　实验的预测目标Y是患者的活动功能得分（Functional Activity Questionnaire, FAQ），该得分是对患者患病程度的常见度量指标。预测变量X是25个主要脑区的体积，这些体积是从结构核磁共振（sMRI）中测量得到的。实验数据来源于 ADNI 数据集。我们根据患者的年龄划分了7个环境 (<60, 60-65, 65-70, 70-75, 75-80, 80-85, >85)，各个环境中分别包含27, 59, 90, 240, 182, 117, 42个样本。我们重复了多个随机种子，每次随机选取4个环境作为训练环境，剩余3个环境作为测试。

　　

　　在 AD 中识别的因果图如图一所示。如图所示，AD 导致的脑萎缩首先出现在海马区（HP）和颞叶中回（TML），进而传播到其他脑区。这一发现与临床研究中发现的海马区、颞叶区是早萎缩脑区这一现象高度吻合，从一个侧面验证了所识别因果图的可靠性。此外，我们还发现，尾状核（CAU）、苍白球（PAL）和海马区（HP）是不稳定脑区，即X_{M}={CAU, PAL, HP}。

　　

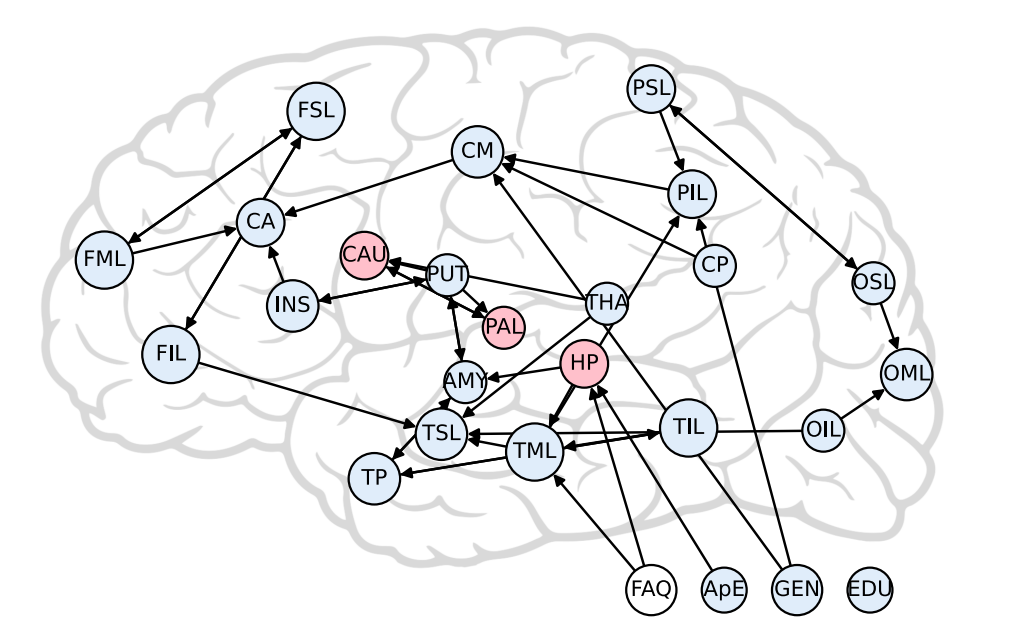
图1. 阿尔兹海默疾病的因果图，红色和蓝色分别表示不稳定脑区和稳定脑区

　　

　　图等价类识别的结果表明，图1中的等价类的个数为25307个，是全部稳定预测器个数2^{22}的0.075%。这一结果说明，对图等价类的搜索能大幅降低复杂度。

　　

　　图2展示了不同方法泛化性能的对比。可以发现，本文方法较已有方法的提升达到15%以上，这充分验证了本文方法的有效性。

　　

图2. 实验结果对比

　　

07 总 结

　　

　　本文提出了一种基于主动干预实现泛化性的理论框架。该框架具有完备的最优性保证、高效的计算算法和较强的可拓展性，在智能医学、具身智能等关键领域有很好的应用潜力。

　　

　　相关问题欢迎联系作者：liumingzhou@stu.pku.edu.cn sunxinwei@fudan.edu.cn

　　

参考文献

[1] Pearl, J. Causality. Cambridge University Press, 2009.

[2] Scholkopf, B., Locatello, F., Bauer, S., Ke, N. R., Kalchbrenner,N., Goyal, A., and Bengio, Y. Toward causal representation learning. Proceedings of the IEEE, 109(5): 612–634, 2021.

[3] Huang, B., Zhang, K., Zhang, J., Ramsey, J., Sanchez-Romero, R., Glymour, C., and Sch¨olkopf, B. Causal discovery from heterogeneous/nonstationary data. Journal of Machine Learning Research, 21(89):1–53, 2020.