2023年4月27日，来自 Google Research 的滕依峰博士访问北京大学前沿计算研究中心，在静园五院做了题为“Pricing Query Complexity of Revenue Maximization”的报告，介绍了在只能获得价值与标价的相对大小的信息条件下、估计价值分布统计量的查询复杂度问题。报告由中心助理教授李彤阳老师主持。

滕依峰博士报告现场

　　拍卖这一重要的经济学模型，在现实中也拥有广泛的应用，例如在线广告拍卖已成为许多互联网公司的主要收益来源。通常计算卖家收益最大化的拍卖需要用到每个买家的价值分布。之前的样本复杂度（sample complexity）的工作假设可以通过真实拍卖（truthful auction）来获得买家的真实价值样本，并研究需要多少样本才能更好地估计买家的价值分布，计算近似最优的拍卖机制。

　　然而，滕博士在报告中指出，由于非真实拍卖的运用以及对买家不正确的建模等问题，现实中买家的真实价值样本通常很难获得，大部分时候我们只能知道买家的价值跟某个预设价格p的大小关系这一二元信息：以标价拍卖为例，买家如果接受了价格p，就说明买家的价值v≥p，否则就是v<p。

　　于是，滕博士及其合作者研究了如果只能通过设置价格p来查询价值与价格p的相对关系时，如何设计查询算法，以及相关的标价查询复杂度（pricing query complexity）的上下界问题。在他们的工作中，他们对常见分布类下（如一般分布、规则分布（regular distribution）和 MHR 分布）常用的统计量（如中位数、均值、垄断价格和分布函数）进行了标价查询复杂度的刻画，与对应场景的样本复杂度进行了比较，体现了标价查询和样本查询能力的异同。在证明过程中，他们提供了规则分布的三个新性质。

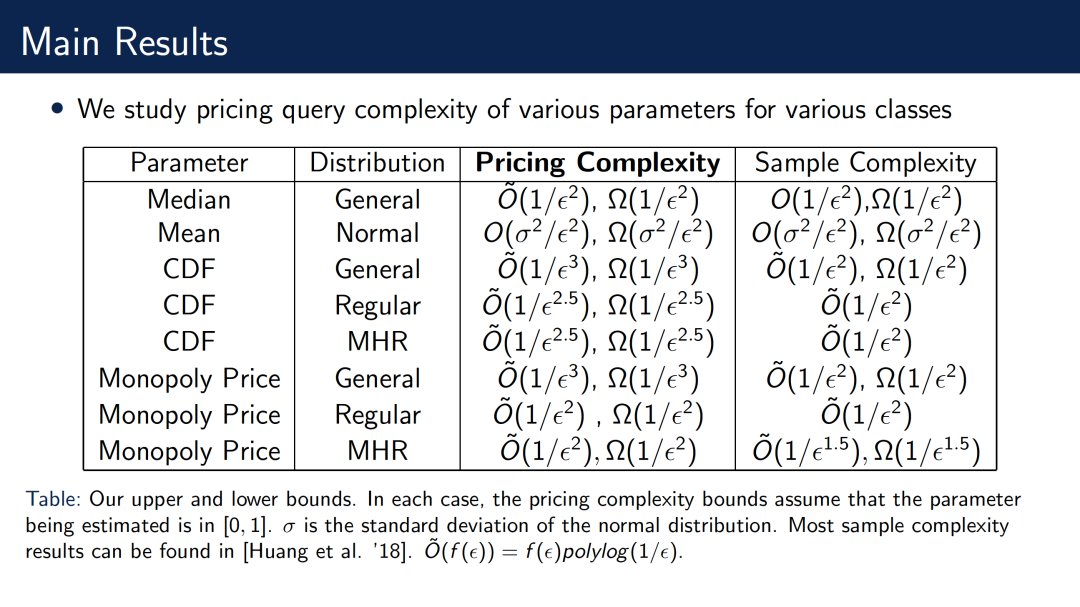
　　滕博士首先介绍了如何利用标价查询估计一个分布的中位数和均值作为热身，方法主要是二分和上置信界算法（upper confidence bound algorithm, UCB）的结合。

　　在对规则分布的垄断价格进行估计的时候，他们注意到规则分布下期望收益关于价格的函数是单峰函数。但是，仅是这一性质并不足以得到有意义的估计，因为峰可以“非常”集中。一个关键的发现是规则分布下对任意4个等距离的点，他们的收益的差不会太远，从而排除了前面的情况。算法的思路仍然是不断地探索垄断价格可能出现的区间，通过排除垄断价格不可能出现的区间来缩小搜索区域。虽然判定规则更为复杂，但每轮最多只需考虑常数个区间。下界的证明用到了信息论的工具，构建了至少需要Ω(1/ε^{2})次查询才能区别的两个实例。

　　在对各分布类的累积分布函数进行估计的时候，为了获得规则分布下的查询复杂度，他们先证明了累积分布函数为凹函数的分布可以用更少的 bit 来进行刻画/描述，继而通过证明规则分布的概率密度函数“几乎”是单调的，来将凹累积分布函数的情况拓展到规则分布的情况。通过对规则分布的描述复杂度进行刻画，他们将估计的上界从一般分布的\widetilde{\Theta}\left(1 / \epsilon^{3}\right)压缩到 \widetilde{\Theta}\left(1 / \epsilon^{2.5}\right)。