2023年3月9日，香港大学的赵琦助理教授受邀访问北京大学前沿计算研究中心，在静园五院做了题为“Commutation and anticommutation in Hamiltonian simulation”的报告，介绍了关于哈密顿模拟中对易与反对易性的最新研究进展。该报告由中心助理教授袁骁老师主持。

赵琦博士报告现场

　　赵琦博士首先引述了著名的诺贝尔物理学奖得主，同时也是量子模拟概念提出者的理查德·菲利普斯·费曼（Richard Phillips Feynman）的名言作为开篇：“Nature isn't classical, and if you want to make a simulation of Nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy.”

　　接着，赵琦博士将目前关于哈密顿量模拟的应用简单总结为三种：

　　1. 实时演化相关（Real-time related）

　　2. 虚时演化相关（imaginary-time related）

　　3. 其他方案（Subroutine in other algorithms）

　　其具体应用见下图：

　　同时，哈密顿模拟算法可以分为两种主要类型，即

　　1. 乘积式（product type）

　　2. 求和式（summation type）

　　如下图所示：

　　赵琦老师介绍介绍了团队的三个最近工作。

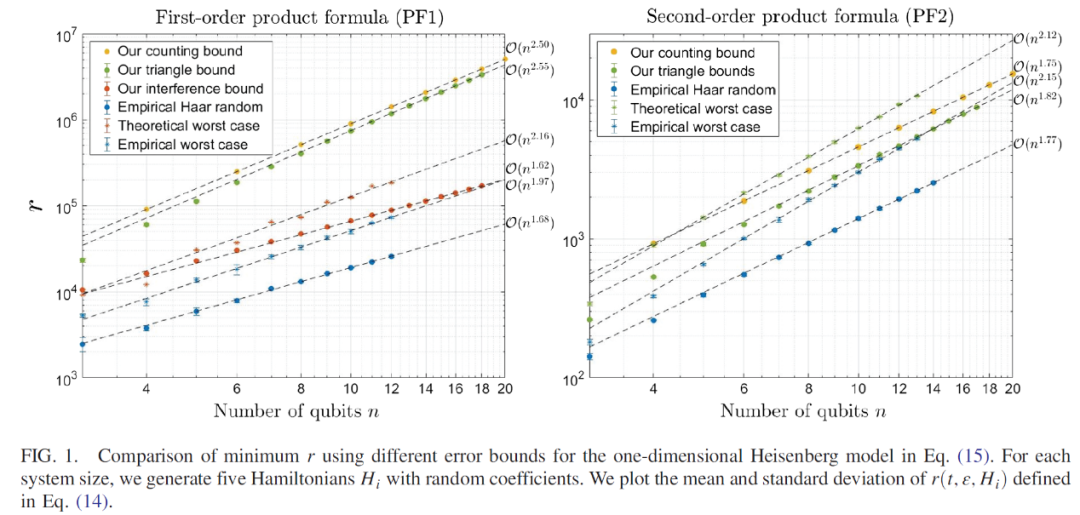
　　首先，数值量子模拟的算法误差（error）通常用实际与理想演化算子之间的谱范数距离来刻画。实际上，这种最坏情况下的误差分析可能是不必要的悲观。为了解决这个问题，赵琦博士团队发展了随机初始状态下哈密顿模拟的平均情况性能理论。他们将平均情况误差（average-case error）与乘法误差的 Frobenius 范数联系起来，并给出乘积公式（product Formula，PF）和截断泰勒级数方法（truncated Taylor series methods）的上界。他们还估计了一般晶格哈密顿量和 k-local 哈密顿量的数字哈密顿量模拟的平均情况误差作为应用。特别是，对于具有n个自旋的最近邻海森堡链，对于 PF 方法和泰勒级数方法，误差从最坏情况下的O(n)二次减少到平均方法的O(\sqrt{n})。数值计算表明，该理论准确地描述了具体模型的平均误差。他们还将我们的结果应用于量子扰频模拟中的误差分析。如下是1维 Heisenberg 模型中该方法与其他方法在哈密顿模拟中的误差 bound 比较，其中 PF1、PF2 分别表示一阶乘积公式与二阶乘积公式：

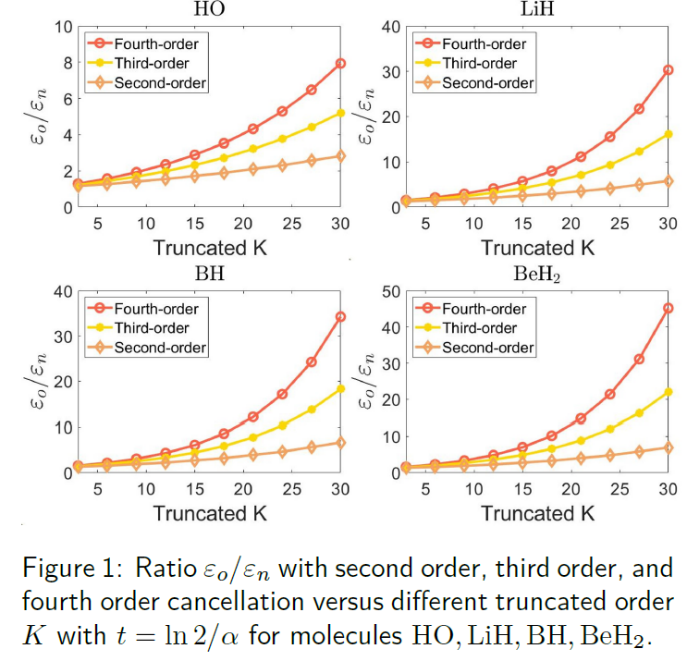
　　此外，量子计算可以有效地模拟多体量子物理的哈密顿动力学，这是经典计算机通常难以完成的任务。困难在于量子算符普遍存在的反对易关系，与经典模拟中臭名昭著的负号问题相对应。直觉上，具有更多对易项的哈密顿量也更容易在量子计算机上模拟，而反对易关系通常会导致更多错误，例如在乘积公式方法中。赵琦博士团队从理论上探讨了反对易关系在哈密顿模拟中的作用。他们发现，与人们的直觉相反，反对易关系也可以降低哈密顿模拟的难度。具体来说，具有相互反对易项的哈密顿量很容易模拟，就像由相互对易项组成的哈密顿量一样。对于一般问题，这种性质进一步用于减少截断泰勒级数量子算法中的算法误差或门复杂性。此外，他们提出了两种修改的线性酉算子组合的方法（modified linear combinations of unitaries method），适用于具有不同反对易程度的哈密顿量。他们数值验证了所提出的利用反对易关系的方法可以显著提高电子哈密顿量的模拟精度。他们的工作揭示了对易和反对易关系在模拟量子系统中的作用。

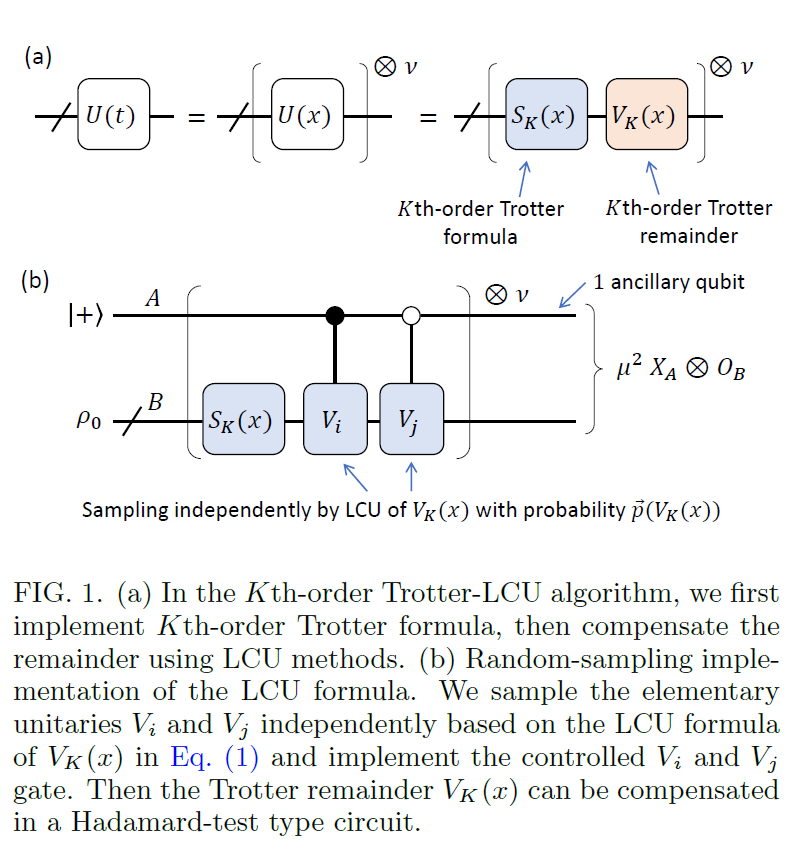
　　接着，赵琦博士团队又提出了使用 LCU 补偿 Trotter 误差的哈密顿模拟算法，这两种算法都有其优点。通过在 K 阶 Trotter 之后添加几个门，他们实现了比2阶 Trotter 更好的时间缩放。他们的第一种算法指数地提高了 K 阶 Trotter 公式的精度缩放。在第二种算法中，他们考虑了哈密顿量的详细结构，并构造了具有换向器缩放的 Trotter 误差的 LCU。因此，对于晶格哈密顿量，该算法具有几乎线性的系统大小依赖性，并二次提高了 K 阶 Trotter 的精度。

　　在报告的最后，赵琦老师提到了课题组目前开放博士后职位（Postdoctoral position opening），欢迎有志之士联系申请：zhaoqi＠cs.hku.hk。

参考文献：

[1] Zhao, Qi and Zhou, You and Shaw, Alexander F. and Li, Tongyang and Childs, Andrew M., Hamiltonian Simulation with Random Inputs. Phys. Rev. Lett. 129.270502 (2022).

[2] Qi Zhao and Xiao Yuan, Exploiting anticommutation in Hamiltonian simulation，Quantum 5, 534 (2021).

[3] Pei Zeng, Jinzhao Sun, y Liang Jiang, and Qi Zhao, Simple and high-precision Hamiltonian simulation by compensating Trotter error with linear combination of unitary operations, HamilarXiv: 2212.04566v1 [quant-ph] (2022).