本文是 AAMAS 2023入选论文 Is Nash Equilibrium Approximator Learnable? 的解读。该论文由北京大学前沿计算研究中心邓小铁课题组与上海交通大学、加拿大 Mila 人工智能中心、英国国王学院、英国伦敦大学学院等机构合作完成，第一作者为邓小铁课题组博士生段志健。本文提出使用函数近似的方法预测纳什均衡，并研究这样的纳什均衡近似器的泛化误差与可学习性。

　　论文链接：https://arxiv.org/abs/2108.07472

01 引 言

　　传统博弈论聚焦于研究对于单个博弈求解纳什均衡，然而当存在大量相似的博弈需要求解时，传统算法无法通过历史数据信息来加速纳什均衡的求解。

　　本文提出利用函数近似的方法，构建一个纳什均衡近似器神经网络，该网络以博弈矩阵作为输入，预测博弈的纳什均衡解。纳什均衡近似器最大的优势在于可以快速并批量求解纳什均衡，其原因在于近似器的计算过程只是简单的神经网络前向计算，而神经网络的计算可以使用 GPU 并行加速。

　　基于函数近似方法，本文在理论方面主要研究纳什均衡近似器的泛化误差与可学习性，在应用方面本文通过实验展示纳什均衡近似器的高效性与潜在应用：热启动传统算法，即为传统近似纳什均衡求解算法快速提供初始化。

02 纳什均衡近似器

　　我们考虑计算正则博弈（两人情况下的正则博弈又称矩阵博弈）的纳什均衡，其中效用矩阵服从一个固定的未知分布。在一组纳什均衡策略下，每个玩家都不能通过单方面改变自己的策略来获得更高的效用。一个例子是在剪刀石头布博弈中，唯一的纳什均衡解是每个玩家以1/3的概率执行剪刀、石头、布中的任何一个动作。

　　我们构建纳什均衡近似器神经网络，以效用矩阵作为输入，预测博弈的纳什均衡解。该近似器可以通过标准机器学习训练方法进行训练，本文给出的训练方法是基于纳什均衡近似误差的批量随机梯度下降算法。纳什均衡近似误差可用于误差衡量一组乘积联合策略对纳什均衡的近似程度，是所有玩家策略的可利用度（exploitability）或动机（incentive）的最大值，其中玩家策略的可以利用度表示该玩家通过改变自己的策略最多能够增加多少效用。由于纳什均衡近似误差几乎处处可微，因此可以作为目标函数，并采用标准的批量随机梯度下降算法来优化近似器参数。

03 理论结果

　　在理论推导方面，我们同样使用纳什均衡近似来衡量近似器的表现。

　　首先，我们推导出纳什均衡预测器的泛化误差。该误差衡量纳什均衡预测器在测试集上的期望表现与训练集上的平均表现的差距。结果表明，给定δ∈(0,1)，我们以至少1-δ的概率满足：

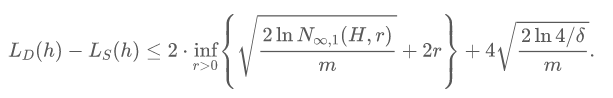
　　其中L_{D}(h)表示近似器h在分布D上的期望表现（纳什近似误差），L_{S}(h)表示近似器在训练集S上的平均表现，m代表训练集大小，N_{∞,1}(H, r)是近似器函数空间H在文章中定义的l_{∞,1}-距离下的r-覆盖数（r-covering number）。从该结论我们可以发现，泛化差距随着训练集样本数量增大可无限趋近于零，这提供了泛化性保障。

　　更进一步地，通过假设纳什均衡近似器神经网络结构表达能力有限，即N_{∞,1}(H, r)有限，我们推导得出了纳什均衡近似器满足不可知 PAC 可学（agnostic PAC learnable）：给定 ε,δ∈(0,1)，当训练集的大小满足

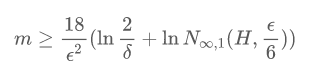
　　时，如果我们基于纳什均衡误差并采用经验误差最小（empirical risk minimization, ERM）算法，我们以至少1-δ的概率可以得到

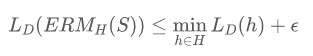
　　该结论表明，当训练样本数量足够大时，我们可以以高概率学到足够接近最优近似器的模型。

04 实 验

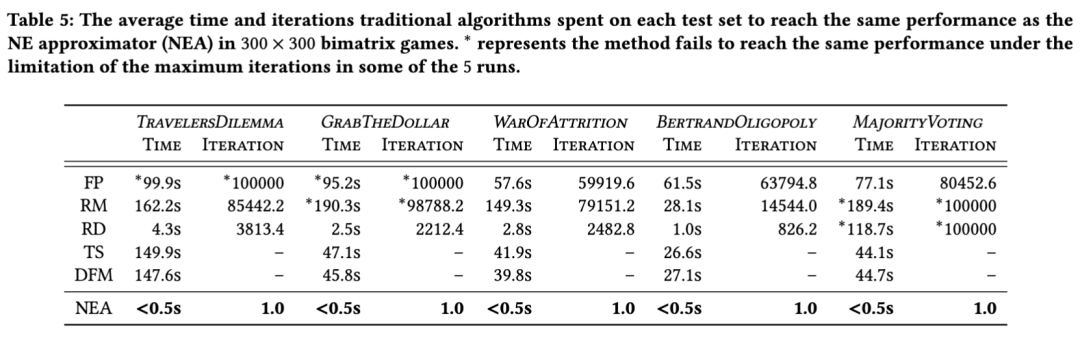
　　在实验方面，我们验证了纳什均衡近似器在求解速度上的高效。我们首先发现，训练完成的近似器在测试阶段可以以很短的时间批量生成大量博弈的近似解，并且传统算法需要大量时间才能达到相当的近似程度。上图为我们的实验中矩阵博弈的实验结果。

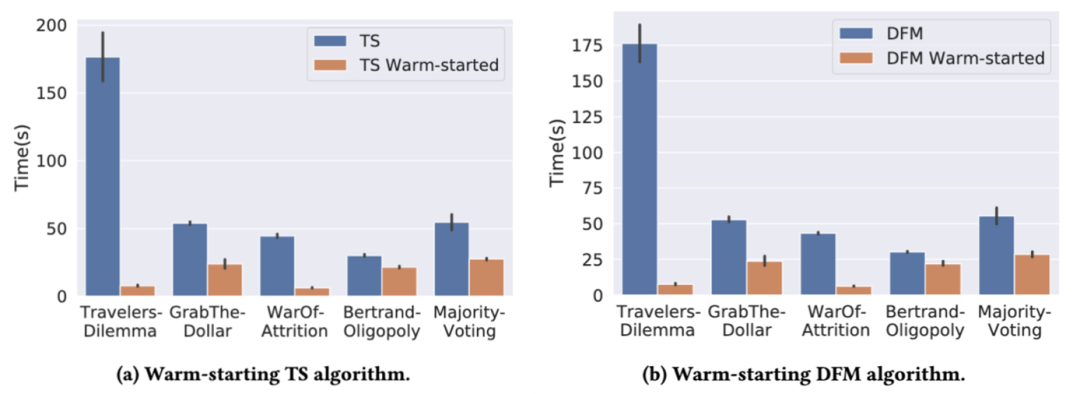
　　此外，我们还发现近似器的一个应用：我们可以将近似器快速计算的纳什均衡近似解作为当前最好的双人博弈近似均衡算法的初始化，来加速这些算法的收敛结果。由于这些算法保障能输出比初始解更优秀的解，因此提供好的初始化总是有用的。实验结果如上图所示，我们大大加快了 TS 算法[1]和 DFM 算法[2]的收敛速度，这样做我们同时结合了数据驱动算法的高效性和传统算法提供的理论保障。

参考文献

[1] Haralampos Tsaknakis and Paul G Spirakis. 2007. An optimization approach for approximate Nash equilibria. In International Workshop on Web and Internet Economics. Springer, 42–56.

[2] Argyrios Deligkas, Michail Fasoulakis, and Evangelos Markakis. 2022. A Polynomial-Time Algorithm for 1/3-Approximate Nash Equilibria in Bimatrix Games. In 30th Annual European Symposium on Algorithms, ESA 2022, September 5-9, 2022, Berlin/Potsdam, Germany (LIPIcs, Vol. 244), Shiri Chechik, Gonzalo Navarro, Eva Rotenberg, and Grzegorz Herman (Eds.). Schloss Dagstuhl - Leibn.