本文是 ICLR 2023 入选 notable-top-5%*的论文 Near-optimal Coresets for Robust Clustering 的解读。该论文由北京大学前沿计算研究中心姜少峰课题组与华为理论计算机实验室合作完成。根据理论计算领域惯例，作者按姓名首字母排序。文章针对一种具有鲁棒性的聚类问题设计核心集构造算法，该算法构造的核心集大小指数级地改进了已有结果，并且逼近理论下界。

　　*对应往年的 Oral。

　　论文链接：https://arxiv.org/abs/2210.10394

01 问题介绍

　　经典的聚类问题，如k-means，旨在寻找一个大小为 k 的点集作为聚类中心，使得所有数据点到聚类中心的距离（的幂次）和这一目标函数最小化。聚类问题是数据分析、机器学习领域的核心问题之一。然而，经典的聚类问题的目标函数经常面临鲁棒性问题，尤其是当数据中有（敌对）噪声时。举例来说，如果在一个数据集中加入一个距离足够远的异常点，聚类算法会被误导，并在该异常点处设置一个聚类中心。因此，本文聚焦于一种具有鲁棒性的聚类问题：带有异常点的聚类问题（clustering with outliers），记为 (k,z,m)-鲁棒聚类，这里m 为一个指示异常点数量的参数。具体来说，给定数据集 X，(k,z,m) -鲁棒聚类问题希望找到一个大小为 k 的聚类中心 C，以最小化如下目标函数：

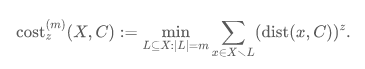
　　在该鲁棒聚类目标函数中，首先把数据点按照到 C 的距离进行排序，然后剔除掉最远的 m 个点，最后在剩下点上套用经典聚类的目标函数。特别地，当 m=0 时，该问题退化成经典的聚类问题。目标函数中的 z 是距离求和的幂次，常见选取 z=1或2，分别对应于 k-median 和 k -means 的目标函数。

　　异常点的出现使得为经典聚类设计的高效算法不再适用，这带来了显著的计算挑战，在大数据计算的背景下尤为突出。因此，我们考虑针对带有异常点的聚类问题的核心集（coresets）。粗略来说，一个ε-核心集是一个极小数据摘要，使得对于任意的聚类中心 C，在核心集上计算得到的目标函数的值与在原数据集上计算得到的值的相对误差不超过 ε。一旦有了核心集，我们只需要将已有的近似算法直接（或经过少部分修改后）运行在核心集上即可得到对于原大数据上问题的近似。自然地，核心集这种基于将大数据化为小数据的方法在大数据计算上，尤其是亚线性算法设计上，也有重要应用。例如，核心集通常可以直接用于得到聚类问题的数据流（streaming）算法、分布式（distributed）算法和动态（dynamic）算法。

02 主要结果

　　本文针对 (k,z,m)-鲁棒聚类问题，设计了一个可在线性时间内构造的大小为

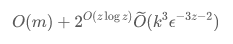
　　的 ε-核心集。其中 \widetilde{O}(f) 隐藏了 polylog(f) 因子。

　　我们的结果显著改进了已有的结果：大小为 (m+k)^{m+k} 的核心集构造算法 [FS12]，以及一个仅达到双重标准近似（即不能保证恰好对 m 个异常点有效）的核心集构造算法 [HJLW18]。此外，我们还证明了任何针对该问题的核心集的大小至少为 Ω(m)。该理论下界结合经典聚类问题的核心集大小下界 \Omega\left(k \epsilon^{-2}\right)[CLSS22] 说明了我们的核心集构造算法已经逼近理论极限。

　　我们还在若干实际数据集中测试了该算法，并与三种 baseline 算法进行比较：简单均匀采样算法（US）、考虑异常点的均匀采样算法（OAUS）以及由 Feldman 和 Schulman 提出的基于敏感性采样算法（Sensitivity Sampling，SS）。我们的算法在所有数据集上都展现了显著的优越性。下图是在多种实际数据集上的性能对比，其中横轴是核心集的大小，纵轴代表在数据集上的实际误差。

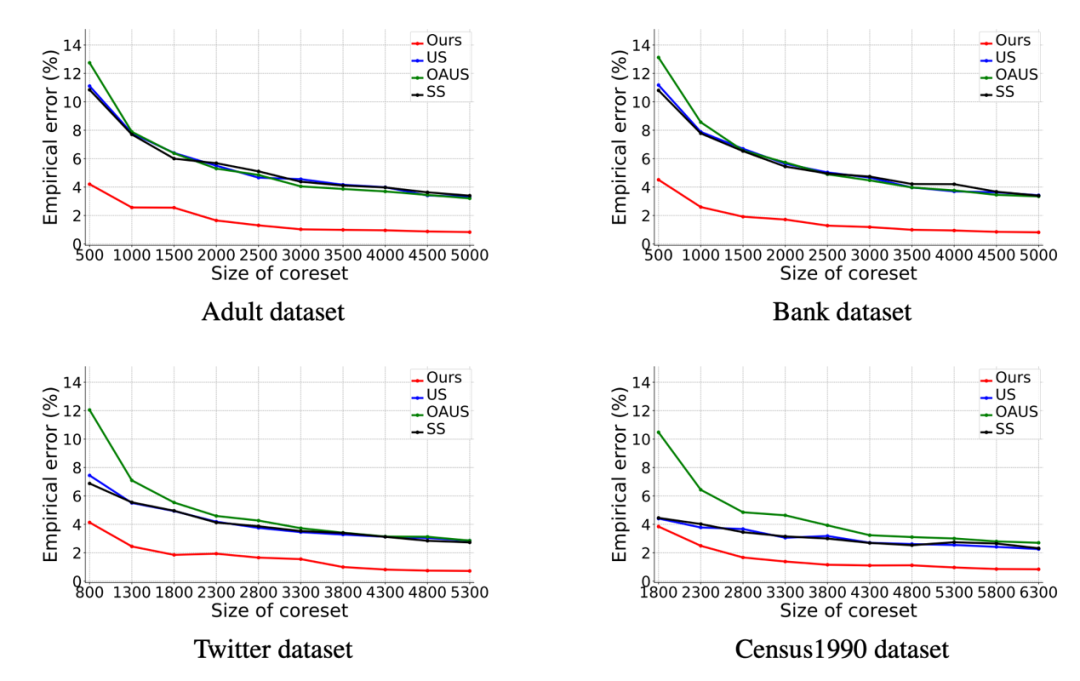
　　另外，我们进一步从实验上证明了我们的核心集可以显著加速已有鲁棒聚类算法。我们选择测试了两种算法：基于经典 Lloyd 的算法（LL）和局部搜索算法（LS）。实验表明，在大小约为1000的核心集上运行算法（记运行时间为 T_{S}）与在原数据集上运行算法（记运行时间为 T_{X}）相比，提速了近百倍（即使加上核心集构造时间 T_{C}），而计算得出的解的相对误差不超过5%。下表是该实验的结果。

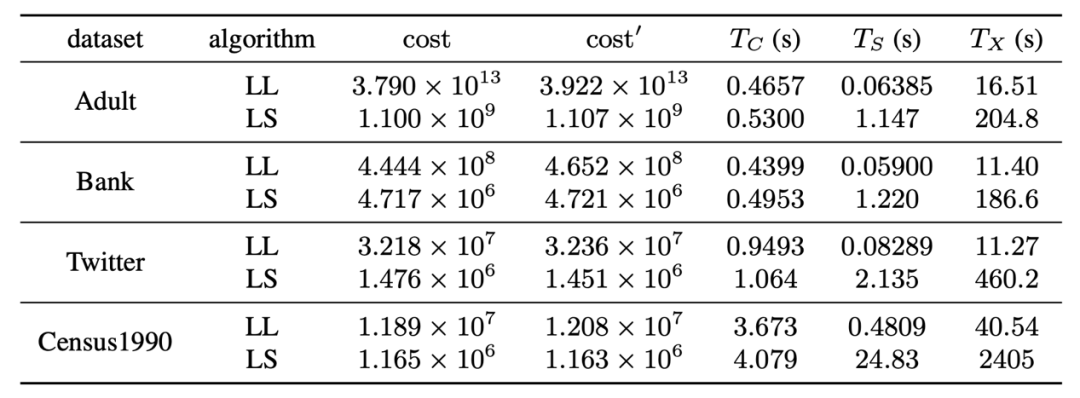
03 算法与分析

　　构造算法：我们的算法基于最近提出的核心集构造算法框架 [BCAJ+22]，大致分为如下步骤：

• 运行已有的三重标准（tri-criteria）近似算法，得到一组近似解C^{*}。
• 根据C^{*}对数据集进行聚类，计算出 m 个到 C^{*} 的最远点，将这些点从数据集中删除并加入核心集S。
• 对于每一个类，利用 [BCAJ+22] 提出的方法将其划分成若干圆环（rings）和若干圆环组成的集合，称为群（groups）。
• 对于每个圆环，均匀采样一定数量的点并加入S。
• 对于每个群，计算一个大小为2的核心集并加入S。
• 输出S作为最终核心集。

　　误差分析：类似于 [BCAJ+22]，我们对圆环和群分别进行分析。然而，异常点的存在为证明带来了不少困难。在这里，我们以z=1的情况为例说明。

　　对于一个圆环R，核心集误差来自于均匀采样。在 [BCAJ+22] 中，对于任意一个聚类中心 C，均匀采样的误差被证明不超过 ε·cost(R,C)（忽略一些极小项），即 ε 乘上所有 R 中的点到 C 的距离和。而由于异常点的存在，我们无法直接利用他们的结论控制误差在 ε·{cost}^{\left(m_{R}\right)}(R,C)之内，其中 m_{R} 为 R 中的异常点数量（相对于 C）。这是因为 {cost}^{\left(m_{R}\right)}(R,C) 可以远小于cost(R,C)甚至接近于 0（当 m_{R} ≈|R|时）。在本文中，我们给出了误差的另一种上界，从而保证除了ε -相对误差之外的误差可以利用 ε·OPT来控制。

　　在群的误差分析中，我们的思路与 [BCAJ+22] 类似。具体来说，我们首先根据群中点的分布情况将群分为染色群和非染色群两类，其中染色群的数量极少。我们称一个群是坏的当且仅当它产生的误差远大于 ε·{cost}^{\left(m_{G}\right)}(G,C)。在 [BCAJ+22] 中，他们证明了只有染色群才可能是坏的群，并且利用加性误差（additive error）控制了坏的群的误差。而当群中存在异常点时，非染色群也有可能是坏的（理由与圆环的情况类似，即 {cost}^{\left(m_{G}\right)}(G,C)可以非常小）。在本文中，我们通过一些几何上的观察，证明了坏的非染色群数量也是有限的，从而证明这一类误差同样可以利用加性误差进行控制。

　　除此之外，我们还需要保证所有关于环/群的误差分析能对所有的异常点数量 t≤m同时成立。这是因为对不同的聚类中心C，每个圆环/群的异常点数量是不固定且无法事先预知的。

参考文献

[BCAJ+22] Vladimir Braverman, Vincent Cohen-Addad, Shaofeng Jiang, Robert Krauthgamer, Chris Schwiegelshohn, Mads Bech Toftrup, and Xuan Wu. The power of uniform sampling for coresets. In FOCS. IEEE Computer Society, 2022.

[CLSS22] Vincent Cohen-Addad, Kasper Green Larsen, David Saulpic, and Chris Schwiegelshohn. Towards optimal lower bounds for k-median and k-means coresets. In STOC, pages 1038–1051. ACM, 2022.

[FS12] Dan Feldman and Leonard J Schulman. Data reduction for weighted and outlier-resistant clustering. In Proceedings of the twenty-third annual ACM-SIAM symposium on Discrete Algorithms, pages 1343–1354. SIAM, 2012.

[HJLW18] Lingxiao Huang, Shaofeng H.-C. Jiang, Jian Li, and Xuan Wu. Epsilon-coresets for clustering (with outliers) in doubling metrics. In FOCS, pages 814–825. IEEE Computer Society, 2018.