本文是 WINE 2022 接收论文 Optimal Private Payoff Manipulation against Commitment in Extensive-form Games 的解读。该工作由北京大学前沿计算研究中心邓小铁教授、陈昱蓉和哥伦比亚大学李毓浩共同完成，入选 WINE 2022最佳学生论文。

　　文章讨论了拓展形式博弈上的 Stackelberg 均衡中跟随者的私有信息操纵问题，在多个设定下完全刻画了跟随者可以通过谎报效用函数来达到的均衡，并给出了跟随者最优谎报策略的多项式时间算法。文章结果说明了在机器学习和数据收集过程中考虑数据提供者基于自己利益谎报消息的必要性。

论文链接：https://arxiv.org/abs/2206.13119

01 概  述

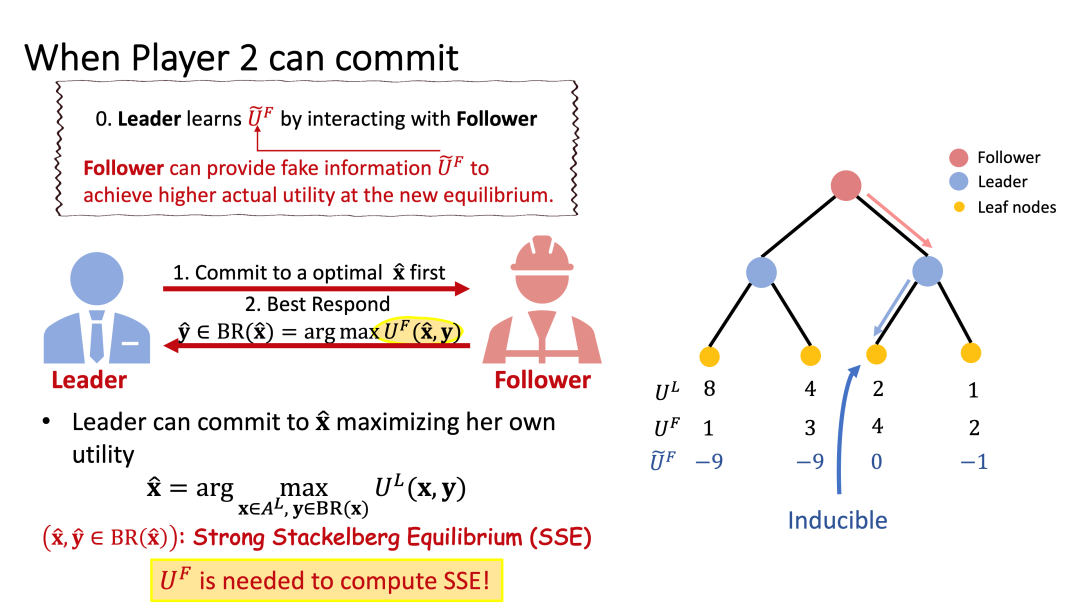
　　Stackelberg 均衡是博弈论解概念之一，在实际中有十分广泛的应用。考虑一个二人博弈，领导者（Leader）会先出策略，跟随者（Follower）在知道领导者的策略之后，会基于理性选择对应的最优反应（best response）策略进行应对。基于跟随者的最优反应函数，领导者就可以通过求解一个两阶段的优化问题得到自己的最优先手策略。领导者的最优先手策略和跟随者对应的最优反应策略即称为一个 Stackelberg 均衡。Stackelberg 均衡下领导者的收益能保证不低于同一博弈纳什均衡下的收益，也即领导者获得了所谓的先手优势。

　　然而为了求解优化问题计算最优先手策略，领导者需要知道跟随者的效用函数，而这在实际情况下往往是跟随者的私有信息。故而领导者需要先通过与跟随者交互来学习跟随者的私有信息，用以计算自己的最优先手策略。这则给跟随者了一个谎报自己效用函数的机会：跟随者可以根据一个虚假的效用函数与领导者进行交互，使得领导者据此计算出的最优先手策略，最后达到的均衡下，跟随者的真实效用会高于真实均衡下的真实效用。

　　一个简单的例子是“大数据杀熟”：现在的一些手机软件，会通过与用户的交互建立用户画像，对不同的用户提供不同的产品和不同的价格。而已有用户会通过建立新账号、更换信用卡等简单的手段修改自己的用户画像，从而达到修改软件获得的效用信息、为自己获利的目的。

　　在本篇工作中，我们主要考虑完美信息扩展形式博弈（extensive-form game with perfect information），研究一个跟随者如何能够找到一个最优的效用函数，通过谎报的方式最大化自己的收益。具体而言，我们将这个过程建模为两个阶段：第一阶段将领导者学习跟随者的过程简化为跟随者汇报一个效用函数；在第二阶段，领导者会根据固定的博弈树、自己的收益函数和跟随者汇报的效用函数，选择一个 Stackelberg 均衡，作为这个博弈的结果。

02 前述知识

　　一个拓展形式博弈（extensive-form game）可由一个博弈树来表示，每个节点会指定一名玩家选择策略，节点上的动作集则是选择一条出边前往下一个子树。玩家的收益由最后到达的叶子结点上的收益来决定。每个玩家的策略一次性决定在每个由他负责的节点上，他将会如何决策。

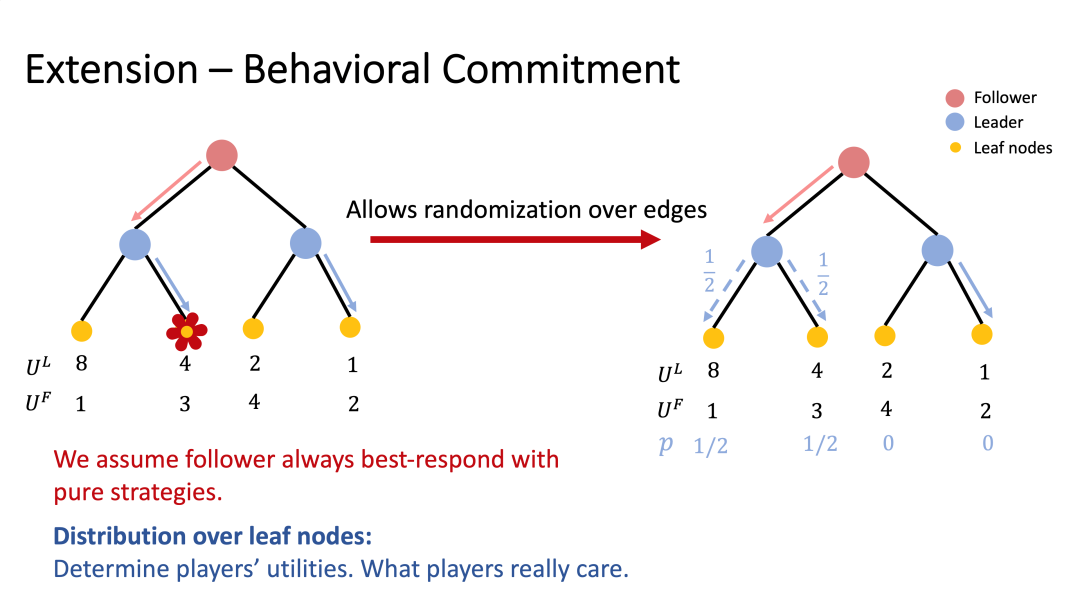
　　我们称这样的策略为纯策略（pure strategy），若在每个节点上，该策略需要明确确定性的一条边的时候；如果允许在每个节点以概率选择哪条边，则这样的策略成为行为策略（behavioral strategy）；我们考虑了领导者的策略集合为纯先手策略（pure commitment）和行为先手策略（behavioral commitment）的情况。

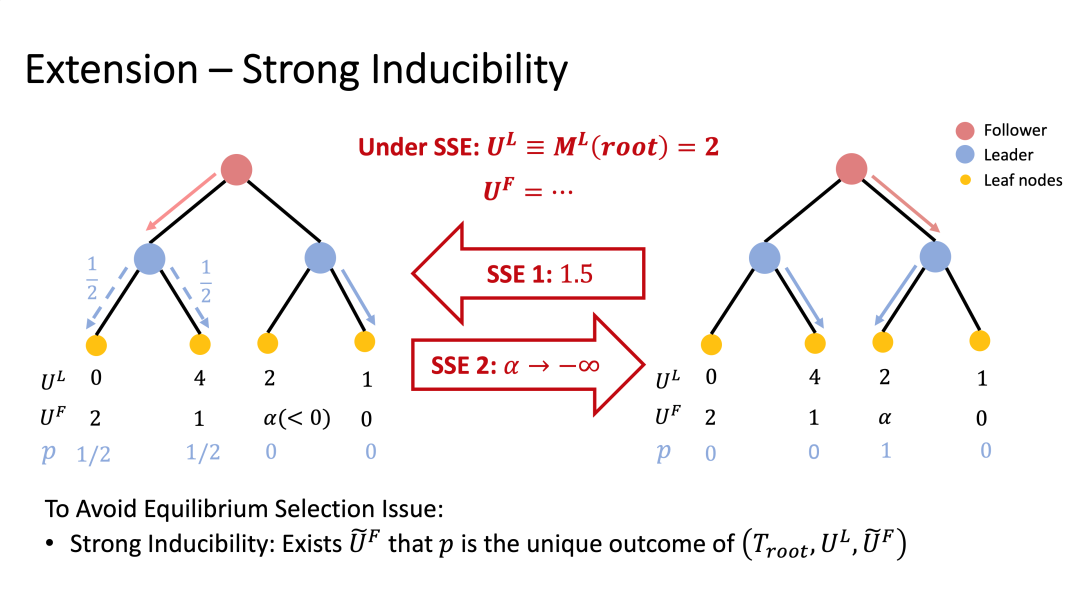
　　考虑到上述考虑的所有策略对最后都会对应于叶子结点上的概率分布，而这些概率分布最终直接决定了玩家的收益。我们将其作为研究跟随者谎报行为的研究对象。我们称一个分布是可被诱导的（inducible），如果存在一个跟随者的效用函数，使得谎报该效用函数后存在一个均衡可实现这个分布；而如果存在一个函数使得所有的均衡都实现这个分布，也就是这个分布就是这个博弈唯一的结果，我们称该分布是强可被诱导的（strongly inducible）。

03 主要结论

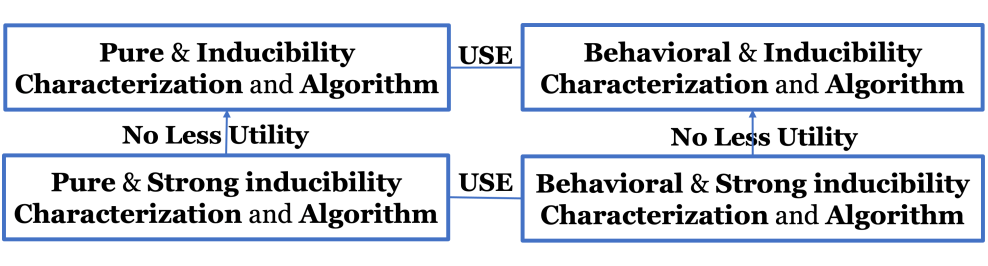
　　对于纯先手策略和行为先手策略两个情况，我们

　　1.  提供了可在多项式时间内验证的可诱导分布和强可诱导分布的完全的刻画；

　　2.  我们为跟随者提供了多项式的算法，使得

　　a.  对于任意一个（强）可诱导分布，构造一个对应的效用函数来诱导它；

　　b.  找到最优的（强）可诱导分布；当最优的强可诱导分布不存在时，我们可找到近似最优的那个。

　　进一步，我们对于同一个博弈四个不同的设定中，跟随者通过谎报能够获得的最优效用进行了比较：

　　3.  关于可诱导性和强可诱导性：我们刻画了两个设定下跟随者的最优函数；我们称这样的博弈满足 Utility Supremum Equivalence (USE) 性质；

　　4.  关于纯先手策略和行为先手策略：我们证明了当领导者可出行为策略时，跟随者的最优收益反而会高于领导者只能出纯策略时的跟随者最优收益。

　　具体的，当领导者只出纯先手策略（pure commitment），而跟随者只考虑可诱导性的情况下，我们证明了一个分布可被诱导，当且仅当领导者在该分布下的效用不小于他的最大化最小收益（maximin value）。这既是纳什均衡收益的下界，也是一个玩家在博弈中能够保证自己一定拿到的最大收益。这一结论说明了，当跟随者可以谎报时，领导者的先手优势荡然无存。

04 总结与展望

　　我们的结果说明了：

　　1.  在信息不对称的情况下，跟随者能够获得更多的权力，并且完全扭转领导者的先手优势；

　　2.  跟随者的谎报能力、其可通过谎报到达的博弈结果以及构造效用函数的方式与领导者的最大化最小值和最大化最小策略有紧密的联系。

　　在拥有海量数据和机器学习技术广泛应用的今天，我们是时候考虑所用的数据是否可用。由于算法结果最终可能会影响到数据提供者自身的利益，数据提供者有动机去提供虚假信息来提高自己的真实利益。研究让数据提供者诚实提供数据的机制和激励相容的机器学习算法变得重要。