本文是 WINE 2022入选论文 Insightful Mining Equilibria 的解读。该工作由北京大学前沿计算研究中心邓小铁课题组完成，受到 Algorand 基金会资助计划的支持。文章聚焦于区块链中经典的自私挖矿攻击，从博弈的角度探讨了应对攻击的策略方法，并进一步刻画了系统在各种策略竞争下的均衡状态。论文作者包括：张梦倩（上海交通大学），李毓浩（哥伦比亚大学），李济宸（北京大学），孔朝哲（北京大学）和邓小铁（北京大学）。

 

　　论文链接：https://arxiv.org/abs/2202.08466

 

　　

01 引 言

 

　　自私挖矿（Selfish Mining）可以说是区块链中最著名的博弈攻击。针对比特币提出的基于工作量证明的共识算法，Eyal 和 Sirer[1]在2014年提出了自私挖矿策略并给出了完整分析，证明比特币的设计不是激励相容的，即攻击者可以通过采用该策略获得比诚实挖矿更多的收益。正常情况下，当节点挖出一个有效区块时，会立即广播使其尽快被全网认可。然而，自私挖矿策略巧妙利用了比特币协议的冲突解决规则，即当出现分叉时，只有更长的子链会被认为是有效的。攻击者通过策略性地隐藏区块、故意制造分叉并诱使诚实矿工在进度落后的子链上浪费算力，提高了其所持算力占比、从而获得更多收益。

 

　　面对自私挖矿攻击， 诚实矿工的收益将大幅受损。此前，大量工作依然基于其他矿池会严格遵守区块链协议的假设，将自私挖矿策略进一步强化或推广，研究和探索了一系列更强有力的攻击策略[2][3]。与之形成鲜明对比的是，在已知系统中存在策略性玩家的情况下，其他矿池的理性反制却很少受到关注。针对该问题的探讨对于研究参与者之间的策略交互和洞悉区块链系统的稳定状态具有重要意义。因此，该工作提出并研究了以下两个问题：

　　1. 矿池能否从博弈的角度策略性地抵御自私挖矿攻击？

　　2. 更进一步，包含多个理性矿池的生态系统最终会达到什么样的均衡？

 

02 远见挖矿策略

 

　　针对问题一，本文从认知层级的角度重新审视自私挖矿攻击，提出了一个称为远见挖矿（Insightful Mining）的应对策略。该策略可以用“螳螂捕蝉，黄雀在后”来概括，其关键想法是，策略玩家可以 通过在自私矿池中安插卧底来获取其隐藏块的数量。基于此， 远见矿池对整个系统的状态有一个清晰的了解，可以清楚地知道其他矿池的挖矿进度，进而做出策略性地反应。具体来说，当系统中的玩家对 当前全局最长链达成共识、开始新一轮挖矿竞争时， 会出现以下三种情况。

 

　　情况一： 诚实矿池生成了第一个区块。 在这种情况下，远见矿池会立即接受这个新区块并且在它后面继续挖矿。

　　情况二：自私矿池生成了第一个区块（并将其隐藏）。 远见矿池通过卧底矿工观察到这一行为后，坚定地跟在诚实子链后挖矿，直到自私矿池释放出所有隐藏的区块。

　　情况三：远见矿池生成了第一个区块。此时， 远见矿池会隐藏这个区块并密切关注诚实子链和自私子链上的区块数量，在接下来的竞争中，如果远见矿池的领先优势大于1，则一直隐藏新挖出的区块；否则，一次性释放出其隐藏的远见子链。

 

　　上述三种情况完整描述了远见挖矿策略。值得一提的是， 即使系统中没有玩家发起自私挖矿攻击，远见挖矿依然可以作为一个独立的挖矿策略被使用，只是此时情况二永远不会出现。

 

03 收益分析

 

　　可以发现，整个系统中使用不同策略的参与者拥有的信息是不对称的。每个矿池都可以用其策略性思考的深度来刻画，而这些思考深度构成了一个迭代的理性层级。

 

　　层级零：诚实矿池作为层级零的参与者，诚实地遵循协议并且拥有的信息只有公开的诚实子链的长度。

　　层级一：自私矿池作为层级一的参与者，认为其他的参与者均为层级零玩家。它采用自私挖矿策略，藏有自私子链，拥有的信息包括诚实子链长度和自私子链的长度。

　　层级二：远见矿池是更为复杂的层级二参与者，它清楚地知道系统中还同时存在层级零和层级一的玩家。得益于安插的卧底，它可以知道系统中所有的信息（即诚实子链、自私子链和远见子链的长度）并且采用远见挖矿策略。

 

　　为了分析不同参与者的相对收益，我们用一个二维向量来表示系统的状态，并且进一步将挖矿建模成一个马尔可夫奖励过程（Markov Reward Process）。 图1展示了系统的状态转移图。

 

图1. 远见挖矿策略下系统的马尔可夫过程

 

　　​令 α 和 β 分别表示自私矿池和远见矿池拥有的算力占比。首先，我们分析了 α=β 的场景并得到以下结论：

 

　　定理1 令 RREV_SM 和 RREV_IM 分别表示自私矿池和远见矿池的期望收益。当 0＜α=β＜1/2 时，RREV_SM (α,β)＜ RREV_IM (α,β) 总是成立。

　　该结果说明，当拥有相同算力时， 远见矿池总是获得比自私矿池严格更大的期望收益。图2展示了二者收益的具体值，可以发现， 当他们的算力大于1/3时（即 α=β＞1/3），远见矿池可以获得几乎所有的收益。

 

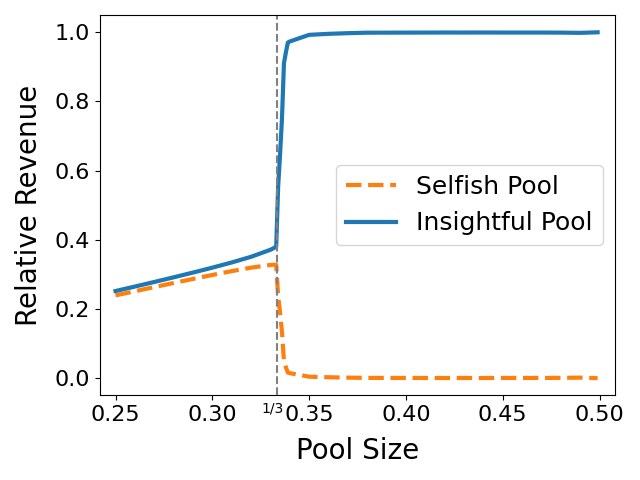
图2. 同算力的自私矿池与远见矿池竞争时的相对收益

 

　　针对 α ＞ β 的场景，图3展示了给定自私矿池算力 α 的情况下，远见矿池为获得更多收益所需的算力阈值。如图所示，借助远见挖矿策略，即使拥有更少的算力也可以获得更高的收益。

 

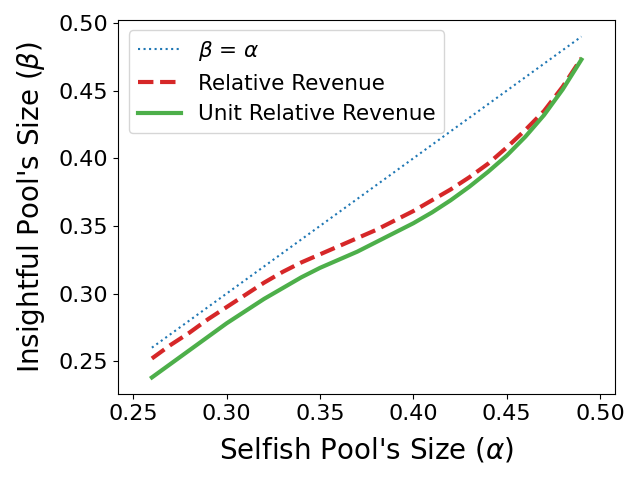
图3. 算力阈值（当远见矿池的算力高于该阈值时可以获得比自私矿池更多的相对收益或单位相对收益）

 

　　上述结果表明， 通过安插卧底矿工所带来的额外洞察力可以大大逆转自私矿池的优势，使得原本利益受损的玩家反败为胜。

 

04 矿池博弈

 

　　进一步，我们探索了系统中包含 n 个策略矿池的场景，并研究其纳什均衡。 在竞争交互的过程中，诚实矿池和自私矿池可能会意识到远见矿池的存在，并学习到该策略。这样一来，所有玩家将处于同一理性层级。 每个矿池 i∈[n] 都可以安排卧底 矿工到其他所有矿池中来监督他们的状态，观察其他矿池是否在隐藏区块，如果是，具体隐藏了多少。

 

　　基于此，每个矿池都可以选择采用改良诚实挖矿或远见挖矿策略，分别用 RHonest 和Insightful 来表示。其中远见挖矿策略与我们之前定义的完全一样，而改良诚实挖矿策略则是诚实挖矿的改良版本：如果发现有人隐藏了区块，改良诚实矿池在面对两条长度相等的子链时会清楚地选择诚实分支，而不是等概率地随机选择其一。

 

　　一个有趣的现象是，在这个挖矿博弈中，任何时候系统中最多只有一个矿池在隐藏区块，这是因为一旦有矿池采取远见挖矿策略、成功挖出了第一个区块并且将其隐藏，其他矿池无论是采取改良诚实挖矿策略还是远见挖矿策略，在这一轮竞争中都不会再隐藏区块。这使得虽然有 2ⁿ 种不同的纯策略组合，但我们可以清楚地分析出每个玩家的期望收益函数，并且给出完整的均衡刻画。

 

　　定理2 对于一个包含 n 个玩家的挖矿博弈 (m₁, ... , m_n) ，其中 m_i 为第 i 个矿池的算力占比。不失一般性，假设 m₁≥...≥m_n。其纯策略纳什均衡 (x₁, ... , x_n) 有以下三种情况：

　　(1) (x₁₌...=x_n=RHonest) 是一个纳什均衡当且仅当 m₁≤ 1/3 成立；

　　(2) (x₁=Insightful_, x₂₌...=x_n=RHonest) 是一个纳什均衡当且仅当 m₁≥1/3，m₂ ≤ g(m₁) 成立；

　　(3)  (x₁=x₂=Insightful_, x₃₌...=x_n=RHonest) 是一个纳什均衡当且仅当 m₁≥1/3, m₂ ≥ g(m₁)成立；

　　其中 g(y):=\frac{-y^3 +2y^2+y-1 }{2y^2+4y-3 } 。

 

　　该定理有以下三个推论：

　　推论1 任何一个 n 玩家的挖矿博弈 (m₁, ... , m_n) 都存在一个纯策略纳什均衡。

　　推论2 对于一个 n 玩家的挖矿博弈 (m₁, ... , m_n) ，如果 m₁ ≤ 1/3，那么所有人都选择诚实挖矿是一个纳什均衡。

　　推论3 对于一个 n 玩家的挖矿博弈 (m₁, ... , m_n) ，均衡状态下 最多只有两个矿池采取远见挖矿策略。

　　

05 总结与展望

 

　　本文针对区块链中经典的自私挖矿攻击，提出了一个称为远见挖矿的应对策略，并进一步给出了挖矿竞争下的系统均衡。 在区块链中，往矿池中插入卧底矿工的行为在区块截留攻击的背景下已经被广泛讨论过[4]， 该工作首次将该想法引入到自私挖矿攻击中 ，为该领域的研究提供了新的启示和思路。

 

　　安插卧底极大地扩展了矿池对抗自私挖矿攻击的策略空间。远见挖矿策略只用到了自私矿池隐藏区块的数量、而没有使用其他信息（比如隐藏区块的哈希值），基于这些由安插卧底获得的额外信息，探索其他更有竞争力的对抗策略是一个值得进一步研究的问题。此外， 将安插卧底的行为扩展到区块链的其他场景也是值得探讨的。

 

参考文献

[1] Eyal I, Sirer E G. Majority is not enough: Bitcoin mining is vulnerable[C]//International conference on financial cryptography and data security. 2014: 436-454.[2] Sapirshtein A, Sompolinsky Y, Zohar A. Optimal selfish mining strategies in bitcoin[C]//International Conference on Financial Cryptography and Data Security. 2016: 515-532.[3] Nayak K, Kumar S, Miller A, et al. Stubborn mining: Generalizing selfish mining and combining with an eclipse attack[C]//2016 IEEE European Symposium on Security and Privacy. 2016: 305-320.[4] Eyal I. The miner's dilemma[C]//2015 IEEE Symposium on Security and Privacy. 2015: 89-103.