第三届国际理论计算机联合大会（International Joint Conference on Theoretical Computer Science-Frontier of Algorithmic Wisdom，IJTCS-FAW）由北京大学讲席教授邓小铁于2020年牵头发起，第三届于2022年8月15日-19日线上线下交互举行。大会由中国计算机学会（CCF）、国际计算机学会中国委员会（ACM China Council）、中国工业与应用数学学会（CSIAM）联合主办，香港城市大学（CityU HK）承办，北京大学前沿计算研究中心、北京大学人工智能研究院协办。

 

　　8月17日，“有意识的图灵机”分论坛由卡内基梅隆大学/北京大学 Manuel Blum, Lenore Blum 教授和北京大学博士生陈昱蓉共同主持。8月16日，青年教师分论坛由北京大学前沿计算研究中心助理教授姜少峰博士主持。小编为大家带来论坛精彩回顾。

 

 

　　有意识的图灵机分论坛精彩回顾

 

Foundations of Multimodal Machine Learning for Intelligence and Consciousness

Paul Pu Liang, Carnegie Mellon University

 

 

　　近年来，人工智能在多种方向取得了丰富的进展，对于图像、声音、文本等信息的识别和处理能力不断增强。多模态人工智能旨在像人类一样通过多种模态接收信息，以及处理、表达。不同模态下的信息有着内在的相互关联，这为综合处理多模态信息提供可能。不同模态的信息会在分布、粒度、信息熵、结构、噪声、相关联想等方面体现出异质性。

 

 

　　不同模态的信息之间可能存在相关性、依赖性等联系，并且在推断中可以形成共同作用，相比于只根据单模态信息进行推断可以做到加强可信度、修正错误等效果。

 

　　讲者介绍了多模态领域的发展历史，可以分为对人类行为的研究、使用计算机模仿人类、与人类交互、利用深度学习这四个阶段。

 

 

　　多模态机器学习存在多种具有挑战性的目标。第一是学习跨越多种模态的表示，以反映出不同模态间的相互作用。第二是找出具有相互关联的不同模态下的信息进行对齐。第三是综合利用多模态信息进行推断。第四是生成某种模态的信息。第五是在不同模态之间进行知识迁移。第六是通过实践和理论更深刻地理解多模态的相互关联。

 

 

　　多模态数据虽然在形式上是异质化的，但可以在抽象的表示空间中具有同质性。如果对各个模态分别进行表示编码映射到同一表示空间，人们希望不同模态得到的表示存在相互关联，称为协同表示。对比学习技术通过训练让同一对象的多模态表示尽量接近，而让不同对象的多模态表示相互远离，可以得到多模态的协同表示。讲者展示了通过图像与文本的协同表示，做到以文本对图像内容进行操作的例子。

 

 

　　讲者将多模态学习与有意识的图灵机相结合，提出 Brainish 模型。通过融合多模态表示，可以建立世界模型（model-of-the-world），综合多模态感知信息，进行行为规划和行为结果的预测。通过将跨模态的表示解码为特定模态下的信息，可以实现联想、翻译、创作等功能。不同模态的信息可以相互实现融合、检索和迁移，取得比单模态学习更好的效果。

 

 

　　最后讲者总结道，多模态学习的核心是数据的异质性与内在的相互关联。多模态学习是人工智能与意识的一个关键的组成部分。

 

Manuel Blum, Lenore Blum教授与邓小铁教授在提问阶段与讲者共同交流

 

 

　　青年教师分论坛精彩回顾

 

An Optimal Separation between Two Property Testing Models for Bounded Degree Directed Graphs

Pan Peng，University of Science and Technology of China

 

 

　　在图分析中，传统的判断问题（例如判断图是否连通）至少需要线性时间，但这个复杂度对于大规模的图是不可接受的，一个新型的决策框架是判断图 G 是否满足性质 P，或者判断 G 是否对于性质 P ε-far。这里 ε-far 是指图 G 需要修改至少 εdn条边才能满足性质 P。

 

　　报告人首先介绍了无向图的性质检测问题很多已有的结果。但有向图的应用更为广泛，例如网站超链接图中，很容易找到出边，但查询入边较为困难。报告人主要考虑建模有向图的性质检测问题，给定一个 d-bounded 有向图 G 和一个性质 P，主要有两种查询模型：双向查询可以查询一个节点的入边和出边；单向查询只能查询出边。

 

　　在上述两个模型下，有一个通用的变换可以将常数查询可测的双向模型转化为亚线性查询可测的单向模型。具体来说，[Czumaj P. Sohler，2016] 证明了一个在双向查询模型中能够在O_{\epsilon, d}(1) 被查询的属性可以在n^{1-\Omega_{\epsilon, d}(1)} 的时间在单向模型中被验证。

 

　　讲者证明了双向模型下，存在常数查询可测的属性 P，其在单向模型下的所需查询下界是O\left(n^{1-\epsilon}\right)，即前述 [Czumaj P. Sohler，2016] 的复杂度是紧的。

 

Ordinal Approximation Algorithms for MMS Allocation of Chores

Xiaowei Wu，University of Macau

 

 

　　报告人考虑的背景是将 m 个不可分割的物体公平分配给 n 个 agents， 每个 agent 对每个物体都有相应的损失函数 c_i(e)≥0，并且损失函数满足可加性，即：c_i(X)=\sum_{e \in X} c_{i}(e) 。对于一个分配 X=(X₁, X₂,..., X_n) 而言，每一个 agent 的损失即为 c_i(X_i)。报告人首先介绍了 MMS 分配问题近年来取得的进展，有学者给出了特定场景下近似算法的上界及下界。

 

　　报告人考虑的第一个模型是不完全信息（只有序信息）的公平分割问题，在此背景下，算法只知道每个 agent 的偏好次序而不知道具体的数值，其近似比需要对满足序信息的所有序列都成立。Round-Robin 算法可以得到 O(2-1/n)的近似比，报告人更为详细的研究了这一问题。当 n 取较小的特定值时，有更为详细的近似比：当 n=2,3 时，报告人给出了最优近似比，当 n=4时，报告人给出了近似比的下界；当 n≥5 时，给出了5/3近似比的算法。

 

　　报告人考虑的第二个模型是算法不知道任何信息，但算法可以查询 agent 的偏好，此时需要设计防策略的算法，使得 agent 没有动机去谎报它的真实偏好。例如 Round-Robin 算法不是防策略算法，因为谎报可能带来好处。报告人解释了谎报的一个重要原因是算法通常需要进行多轮选择，因此每个 agent 应当只选择一次，但可以选 a_i 个。基于上述规则，报告人给出了 O\left(\log \left(\frac{m}{n}\right)\right) 近似比的确定性算法和 O(\sqrt{\log n}) 近似比的随机算法。

 

The Power of Uniform Sampling for Coresets

Xuan Wu，Huawei TCS Lab

 

 

　　核心集（Coreset）是一种数据摘要技术，不仅可以有效提高算法效率，还能提升泛化能力、防止过拟合，这在图像处理、NLP 等问题中应用广泛。报告人首先介绍了核心集技术的众多优势，例如可以将传统的算法应用到亚线性模型中去，例如流式数据，分布式数据，动态数据等。此报告中介绍的核心集技术的突出特点是应用广泛，并且对于各类聚类问题给出了更好的核心集大小的界，例如带容量限制的聚类和带公平性限制的聚类，H-minor-free 图上的聚类和 Wasserstein 重心等等。

 

　　在先前工作中，重要性采样是最广泛使用的技术，但其计算复杂、分析困难，且难以处理带容量限制和公平性限制的聚类。报告人采用了新的框架，先预处理然后均匀采样。具体来说，在该算法框架中，先对数据进行层次划分，再对损失较大的层及其邻居层进行均匀采样，而对其余层构造仅需要2个样本的核心集。相比之下，该方法更易于分析，且适用于带约束的聚类，并可以直接推广到其他度量空间。

 

Graphical Resource Allocation with Matching-Induced Utilities

Bo Li，Hong Kong Polytechnic University

 

 

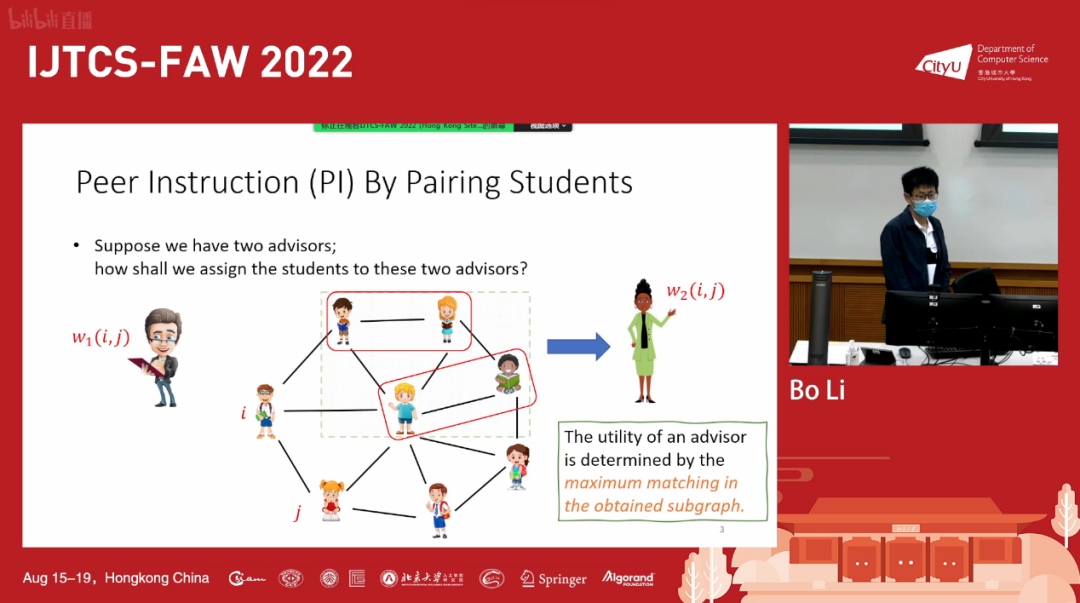
　　基于图的分配问题有着广泛的应用，例如在设计同侪辅导的匹配时，不同的导师对学生的匹配有着不同的偏好，此时每个导师的评分即为子图中的最大匹配。具体而言，我们需要计算一个分配 X=(X₁，...，X_n)，使得资源 X 被公平的分配给 n 个 agents。讲者主要关注两个公平性的指标：Maximin Share（MMS）和 Envy-freeness 1（EF1）。

 

　　报告人首先考虑 MMS 指标。对于同质的 agent，MMS 公平退化为一个 max-min 问题，具体而言，我们需要找到一个划分使得最小的评估函数 G(X_i) 最大，这是一个 NP-hard 问题，有一些启发式的算法，但没有给出近似比的上界。在讲者的工作中，首先获得图 G 一个最大匹配 M*，然后获得 M* 的 max-min 划分 (M₁，...，M_n) 并不断的降低最大划分的权重，直至达一个合理的范围。该算法可以达到1/8的近似比。然而，在该算法中，保证 MMS 公平的代价是社会效益（social welfare）遭受损失，具体而言，任何有限近似比的 MMS 公平算法都无法避免无限近似比的社会效益。因此 MMS 对社会效益而言不是一个好的指标。

 

　　报告人考虑另一种公平性指标 Envy-Free 1。EF1 的分配始终存在并且很容易找到 [Lipton et al.，2004]。因此讲者关注的另一个问题是: 如何在满足 EF1 前提下获得最好的社会效益？在同质 agent 的情况下，报告人给出了求解 EF1 的方案且常数近似比的算法，在异质 agent 下，报告人给出了二次近似比的算法。

 

A Polynomial Time Algorithm for Submodular 4-Partition

Chao Xu，University of Electronic Science and Technology of China

 

 

　　报告人考虑 k- 划分的次模优化问题，给定一个集合 X 及其定义在上面的次模函数 f，需要将该集合划分为 k 个子集，使得在子集上的 f 取值最小。k- 划分次模优化问题有着广泛的应用场景，例如在图 G 中定义 f(S) 为一个端点在 S 内另一个端点在 S 外的边的数量，图 G 的最小 k- 割问题便转化为一个 k- 划分次模优化问题。在超图中亦可以定义类似的最小 k- 割问题。

 

　　图和超图的最小k割问题以及次模函数最小 k 划分问题都有大量的研究，主要使用的技术有：

　　1. Deletion，在 X 上求解 j- 划分问题，在 V\X 上求解 (k-j)- 划分问题；

　　2. Contraction，寻找一个小的子集 X，使得 X 不跨过最小 k- 划分，因此可以压缩 X 得到更小的问题；

　　3. Tree Packing。

 

　　报告人改进了 k=3时的次模划分算法的证明，从而将其推广到 k=4。并给出了当次模函数满足对称性时5划分优化问题的时间复杂度上界。

 

Survivable Network Design: Group-Connectivity

Yuhao Zhang，Shanghai Jiao Tong University

 

 

　　如何设计容错的网络拓扑是一个广受关注的问题。可以使用连接强度 k 来定义抗毁性，即拓扑图上 k-1 个连接被破坏后，该网络仍能正常工作。给定图 G=(V，E) ，每条边对应一个代价 c_e，我们需要连接边来满足给定的连通需求 Q 和连接强度 k。

 

　　先前这方面的工作大多数考虑点对点的连通需求，而关于 group 对 group 连通的问题，只在一些特殊情况能得到对数多项式的近似比，对一般的情况，只有双标准近似（bicriteria approximation）的算法，虽然花费的代价达到对数多项式级别的近似比，但连接强度无法保证达到k。

 

　　报告人的工作获得了第一个非平凡的近似算法，对于常数大小的任意 k 可以达到对数多项式级别的近似比。报告人介绍了这一工作所使用的工具和技术，包括连通性增强、基于割的树嵌入、CGL 迭代舍入等。