本文是 NeurIPS 2022入选论文 Eliciting Thinking Hierarchy without a Prior 的解读。该论文由北京大学前沿计算研究中心孔雨晴课题组完成，其中论文作者黄致焕为北京大学图灵班21届毕业生，李韵祺、张宇博、吴瑾昭为北京大学图灵班22届毕业生。文章研究了如何在没有任何先验信息的情况下汇总人群的观点，使得即使在大部分人的观点产生系统性偏差的情况下，高质量的观点仍然可以被有效识别。

 

　　论文链接：https://arxiv.org/abs/2109.10619

　　网站链接：https://elicitation.info/classroom/1/

 

01 引 言

 

　　“小圆的半径是大圆的1/3，小圆绕大圆滚动一圈，请问小圆自转了多少圈？”

　　“恰似你的温柔原唱是谁？”

　　 ……

 

　　如果你上述两题的答案是“3”“蔡琴”，那么我们有一个好消息和一个坏消息要告诉你。好消息是：你和大多数人一样，坏消息是：你们都错了。

 

　　以上情况并不少见。在已知客观答案的情况下，自然可以判断大多数人的答案是否正确。然而，在没有任何先验和验证的情况下，我们无法分辨到底是跟随“群体的智慧”还是相信“真理掌握在少数人手中。” 正如围棋中的 “本手、妙手、俗手”，外行很难分辨。

 

　　这引入了本文研究的核心问题：“如何在没有先验的情况下评估答案质量？”

 

　　以圆圈问题为例，我们收集到答案的分布图为：

 

 

　　回答者中，134人回答“3”，11人回答“1”，8人回答“2”，16人回答“4”，27人回答“6”，21人回答“9”。

 

　　正如前文所言，在没有先验的情况下，很难对这些答案采取支持度以外的排序方式。Prelec ^[1], Prelec et al. ^[2] 通过在单选题中额外询问回答者对各个选项分布的预测，进而构造先验信息，并汇总答案为支持度“令人意外地高”的选项，并实验证明该方法比多数决有效。Rothschild and Wolfers ^[3] 在民调时除了询问“你会选谁”，还额外询问选民“你觉得谁会得到更多的支持”，并实验证明额外信息具有更高的信息量。

 

　　类似地，我们采用了一套基于填空题的问卷调查方式：

　　“你的答案是？”

　　“你觉得别人会答什么？”

 

　　与之前工作不同，在以上框架下，询问者无需任何先验设计选项，回答者无需提供分布信息。针对答案的汇总，Kong and Schoenebeck ^[4] 提出一个猜想：“专业度高的人可以预测专业度低的答案，反之不然。”

 

　　这个猜想和行为经济学有限理性理论中的等级 k（Level-k）^[5] 以及认知等级（Cognitive Hierarchy）^[6] 理论相似，都认为人在逻辑思考推理中存在不同的等级。等级 k 和认知等级理论认为高等级知道低等级的存在并采取针对低等级的最优策略。

 

　　我们将认知等级理论推广到非策略游戏场景，并结合以上猜想提出了一套新的信息汇总框架。该框架可以在没有任何先验的情况下：

　　1. 学习人群的思考等级；

　　2. 排序答案，使得高等级的答案虽然不一定被大多数人支持，但会被专业度更高的人支持。

 

02 算法模型

 

　　收集完回答者的答案以及他们对他人答案的猜测/预测后，我们将构建如下矩阵。

 

　　答猜矩阵

 

　　对于一个问题，令 A 为所有可能的答案的集合。定义答猜矩阵 M 为大小是 |A| x |A| 的矩阵，其中：

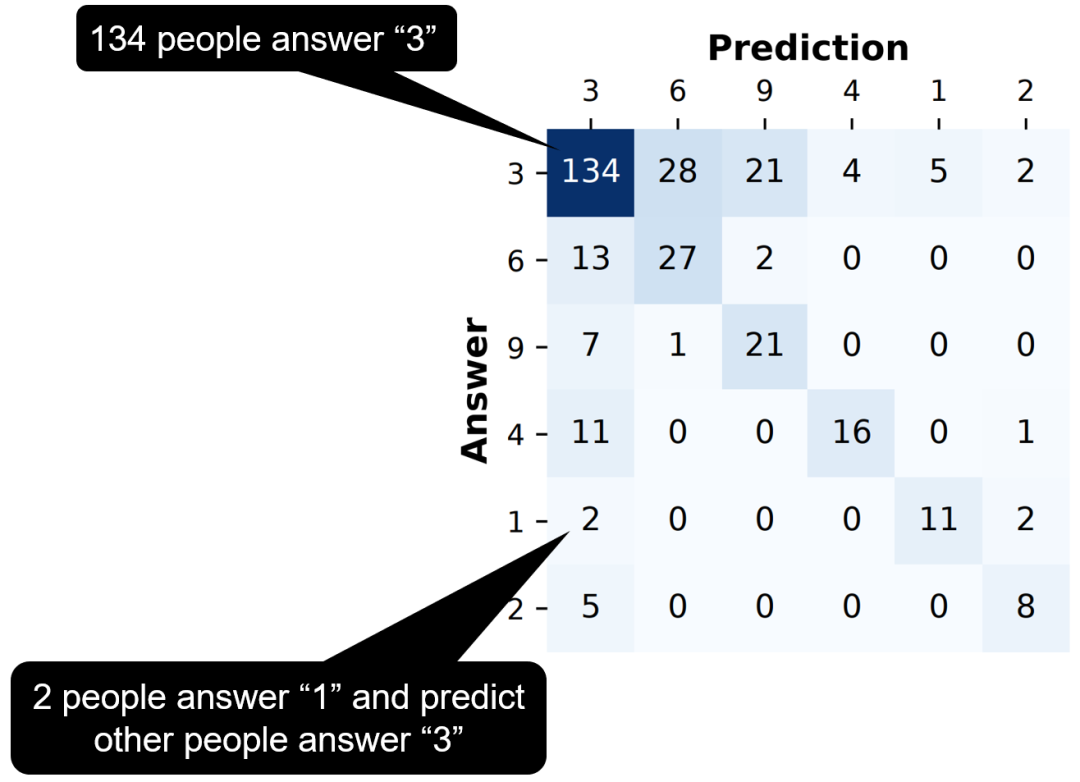
• 　　非对角线：第 x 行第 y 列表示有多少个回答者回答了第 x 个答案并预测了第 y 个答案。例如，下图中第五行第一列代表有两个人回答“1”并认为别人回答“3”。
• 　　对角线：第 x 行第 x 列表示有多少回答者回答了第 x 个答案。例如，下图中第一行第一列代表有134个人回答了“3”。

 

 

　　什么样的答案顺序是好的？

 

　　为了找到专业度更高的答案，我们需要对答案进行排序。由于专业度高的人可以预测专业度低的答案，反之不然，因此我们需要让回答排名靠前的答案并预测排名靠后的答案的回答者尽量多。具体来说，我们的默认算法（default algorithm）将找到最优的答案顺序以最大化答猜矩阵右上角元素的平方和：

 

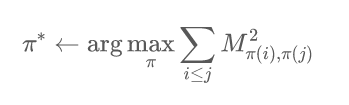
　　这里 π 为答案的顺序，其中 π(i) 表示排名第 i 的答案。我们的论文提出了一套理论框架验证了该算法可以在一些假设下学习到思考等级。具体内容请参考论文原文。

 

　　下图即为圆圈问题最优答案顺序下的答猜矩阵。其成功给了正确答案“4”最高等级。

 

 

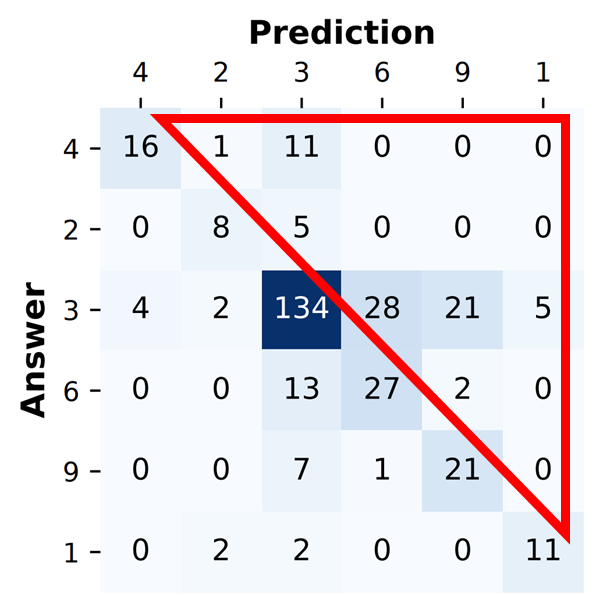
　　除了默认算法之外，我们还提出了一个变体算法（Variant algorithm），由于实验效果不如默认算法在此不再赘述。

 

03 实 验

 

　　我们选取了数学题、围棋死活题、常识题和汉字读音题四种类型进行实验。

 

　　在四种类型的152个问题中，我们的算法在134个问题中得到了正确答案，而简单多数仅答对116个问题，其具体结果如下表所示。

 

 

 

　　数据收集及处理

 

　　所有的实验使用线上问卷的方式进行。在数据处理中，我们将相同的答案进行了合并（如：‘0.5’和‘50%’），并且忽略了不到3%的回答者报告的答案和“不知道”。剩下的答案组成了答案集 A，其大小为 |A|。我们依次建立答猜矩阵并进行排序。

 

　　案例分析

 

　　常识题

　　我们介绍两个具有代表性的问题。

　　第一个问题是中国和朝鲜的界河。在82个回答者中，74个回答了鸭绿江。然而，很少有人知道图们江也是中国和朝鲜界河的一部分。除此之外，松花江是中国东北一条非常有名的河流。我们的算法成功得到了正确答案，并找到了“鸭绿江和图们江->鸭绿江->松花江”的知识等级。

 

 

　　第二个问题是中世纪的新年是什么时候，最简单的想法是和现在的新年一样：1月1日，而这显然是错误的。也有些回答者进行了思考，选择了12月25日，圣诞节。但是算法得到的排名第一的答案是4月1日，这也是正确答案。我们的算法成功得到了正确答案，并找到了“4月1日->12月25日->1月1日”的知识等级。

 

 

　　汉字读音题

　　第一个问题是"睢”的读音。大部分人对“雎”更熟悉，因为这个字在诗经中的著名歌谣“关雎”中出现。二者在字形上非常相似。除此之外，也有回答者将其和“zhì（雉/稚）”或者“zhuī（锥）”混淆，而得到错误答案。我们的算法输出了正确答案（suī），并找到了“suī->jū->zhì->zhuī”的知识等级。

 

 

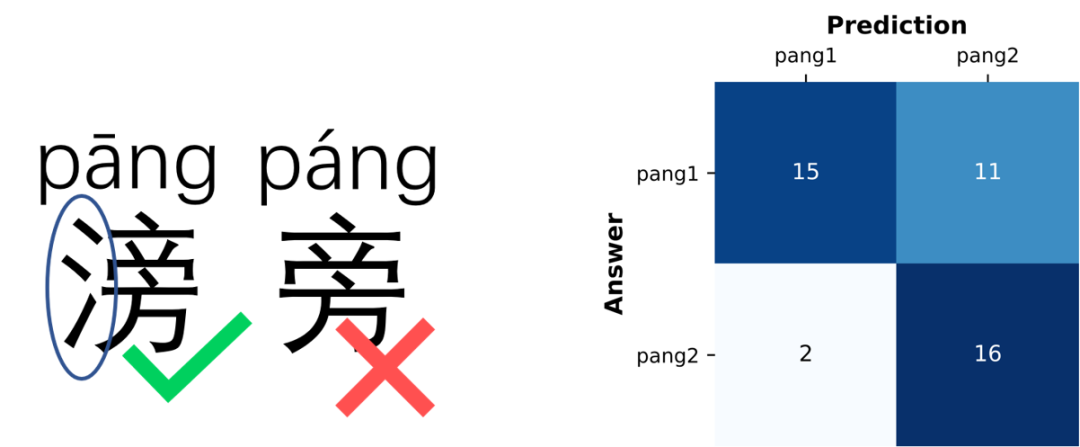
　　第二个问题是“滂”的读音。当我们不知道一个字的具体读音时，会倾向于读半边，因此大部分的回答者报告了错误的答案“páng”，即“旁”的读音，而非正确答案“pāng”。我们的算法在找到正确答案的同时输出了知识等级“pāng->páng”。

 

 

　　数学题

　　我们在这里介绍一个非常著名的数学问题——蒙提霍尔问题（也称作羊车问题、三门问题）。这个问题出自一档电视节目，在这个节目中参赛者会看见三扇门，其中一扇的后面是汽车，另外两扇门的后面是山羊。选中汽车的门就可以获得一辆汽车。在参赛者选定一扇门后，主持人不会立刻打开那扇门，而是会开启剩下的两扇门种有山羊的那扇，随后问参赛者要不要换另一扇还没打开的门。问题是：换一扇门后赢得汽车的概率是多少？

 

　　许多人会这样思考这个问题：一开始每扇门有汽车的概率都是1/3，现在排除了一扇门，那么剩下的两扇门有汽车的概率都是1/2。这个推理的错误在于，主持人并不是随机挑选了一扇门排除，而是挑选了你选的那扇门以外的一扇门来排除。事实上，换一扇门赢得汽车的概率也就等于你一开始没有选中汽车的概率，也就是2/3。那些被这个问题坑过的人和仔细思考过这个问题的人都可以顺利地推出2/3的答案，并知道大部分人会选1/2。我们的算法成功得到了正确答案，并给出了“2/3->1/2->1/3”的思考等级。

 

 

　　围棋题

　　我们挑选了若干难度各异的死活题目，在此我们选择一个“本手”和“妙手”都比较明显的题目进行介绍。

　　警告：以下内容非围棋专业人士谨慎阅读。

 

 

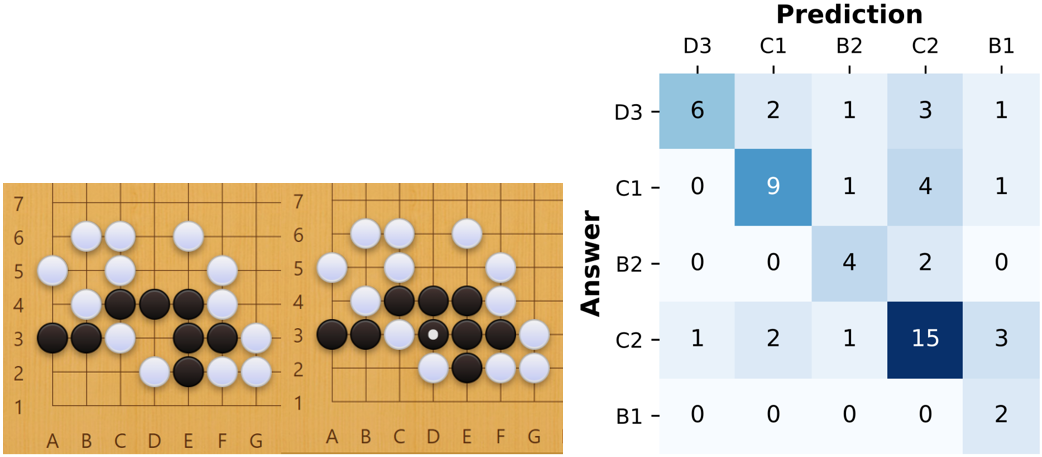
　　在这一题中，一些围棋入门者的第一反应会是 C2 打吃，理由是吃掉黑棋中包围的这块白棋看起来就可以做活。然而 C2 打吃并不足以吃掉白棋，白棋下 E1 即可从容接走自己 D2 的白子。

• 　　之后若黑选择 D3 提，则白 D1 接。此后 C3 处并不能做出眼，而角落里 2x2 的空间白棋只要点一个子黑棋就成为死棋。
• 　　此时黑棋唯一的妙手是 B1 试图做眼，白棋只能下 A2 破坏黑棋的双眼，而后黑下 D1 来做成劫活。

 

　　有些经验的初学者可能会选择 C1 尖，是一种更加灵动的走法，此时白若继续 E1 试图接走 D2 的白子，黑可以下 D1 挫败白棋的计划，看起来是不错的选择。然而白可以下 C2 后去杀 A3B3 的黑子，从而曲线救出 C3D2 的白子。

 

　　聪明的棋手可以注意到，可以有净活的做法。正解是黑 D3 挤，乍一看和 C2 打吃并没有本质差别。但若此时白棋仍下 E1，黑棋有如下的解法：

　　1. 首先下 D1 来逼迫白棋 C1 提子；

　　2. 然后下 B1 来做眼，此时白棋有几种应对策略：

　　a. 白 A2 破眼，黑 C2 提子，同时将死 C1，D2 的白子；

　　b. 白 D1 接，黑 C2 提子逼迫白 F1 接，随后黑 A2 点出双眼做活；

　　c. 白 C2 接完全不可行，会被黑 B2 杀死。

　　（注：黑先下 D1 是必要的，先下 B1 的话白棋可以 D1 接，此后黑棋无法做出双眼。）

 

　　可以看出，虽然解的空间其实很小，但得出正确的解却需要很长的思考。黑 D3 挤是一个不符合常规的“围棋美学”的走法，因此在预测的时候初学者很少会想到走这里。而走 D3 的人却可以很轻松地料到初学者会走到 C2，C1 的位置。

 

　　我们的算法也成功地在没有任何先验的情况下给出了“D3->C1->B2->C2->B1”的等级。

 

 

04 总结与展望

 

　　我们提出了一套新的信息汇总算法。该算法无需任何先验信息，只需要每个人回答后额外提供对别人答案的预测。我们实验证明了在大多数情况下，即使大部分人都错了，该算法仍然可以汇总得到正确答案。除此之外，我们的算法还可以对人们提供的答案进行“思维分层”，展现了人们的“思考路径”。

 

　　未来，我们希望可以将该方法运用在问答平台的答案排序上，以及其它需要汇总人群信息的场景。例如在收集人群对决策的建议和观点时，我们希望可以通过展现人群的“思考路径”来更深入地理解人群的观点。我们甚至可以比较人和 AI 的思考等级。另一个有趣的拓展方向是汇总连续答案空间的信息，包含汇总人群的预测，对艺术品的估值，或者对房价的估计。

 

　　最后，我们向实验中所有的参与者表示感谢。

 

参考文献

[1] D. Prelec. A Bayesian Truth Serum for subjective data. Science, 306(5695):462–466, 2004

[2] Dražen Prelec, H Sebastian Seung, and John McCoy. A solution to the single-question crowd wisdom problem. Nature, 541(7638):532–535, 2017.

[3] David M Rothschild and Justin Wolfers. Forecasting elections: Voter intentions versus expectations. Available at SSRN 1884644, 2011.

[4] Kong, Yuqing and Schoenebeck, Grant. Eliciting expertise without verification. In Proceedings of the 2018 ACM Conference on Economics and Computation, 195–212 (2018).

[5] Dale O Stahl and Paul W Wilson. On players’ models of other players: Theory and experimental evidence. Games and Economic Behavior, 10(1):218–254, 1995.

[6] Colin F Camerer, Teck-Hua Ho, and Juin-Kuan Chong. A cognitive hierarchy model of games. The Quarterly Journal of Economics, 119(3):861–898, 2004.