第三届国际理论计算机联合大会（International Joint Conference on Theoretical Computer Science-Frontier of Algorithmic Wisdom，IJTCS-FAW）由北京大学讲席教授邓小铁于2020年牵头发起，第三届于2022年8月15日-19日线上线下交互举行。大会由中国计算机学会（CCF）、国际计算机学会中国委员会（ACM China Council）、中国工业与应用数学学会（CSIAM）联合主办，香港城市大学（CityU）承办，北京大学前沿计算研究中心、北京大学人工智能研究院协办。

　　

　　8月18日，青年博士生分论坛由北京理工大学刘金艳助理教授主持。小编为大家带来论坛精彩回顾。

 

 

精彩回顾

　　

Optimal Rates of (Locally) Differentially Private Heavy-tailed Multi-Armed Bandit

伍玉莲，阿卜杜拉国王科技大学

 

 

　　多臂老虎机（multi-armed bandits）问题是概率论中的一个经典问题，也属于强化学习的范畴，该问题在医疗，经济，社会科学和临床研究中有着广泛的应用。然而，在实际环境中有些数据涉及隐私，从而引出了两个具有挑战的问题：如何保护这些数据的隐私以及如何汇总和学习敏感数据。解决上述问题的一个方法是利用差分隐私（differential privacy，DP），并在近几年吸引了众多学者的关注和研究。然而，讲者发现在很多现实情境下奖励分布满足重尾分布（heavy-tailed distribution），并不是之前研究中所假设的有界或者高斯分布。因此，讲者提出并研究了在不同 DP 模型下的满足重尾奖励分布的多臂老虎机问题。

 

 

　　在全局 DP 模型中，讲者通过提出一个具有私有性、鲁棒性的 "置信度上界"（Upper Confidence Bound ，UCB）算法来提供一个接近最优的结果，并通过一个私有鲁棒的逐次消除（Successive Elimination ，SE）算法来改进这个结果。除此之外，讲者还给出了下限来证明改进后的算法与实例相关的后悔值（regret）是最优的。在局部 DP 模型，讲者也提出了一种算法，它可以被看作是 SE 算法的局部私有和鲁棒的版本，并且讲者证明了该算法在与实例相关和与实例无关的后悔值都达到了（接近）最优。此外，讲者还总结了有界/次高斯奖励的私有 MAB 问题与重尾奖励之间的差异。

 

 

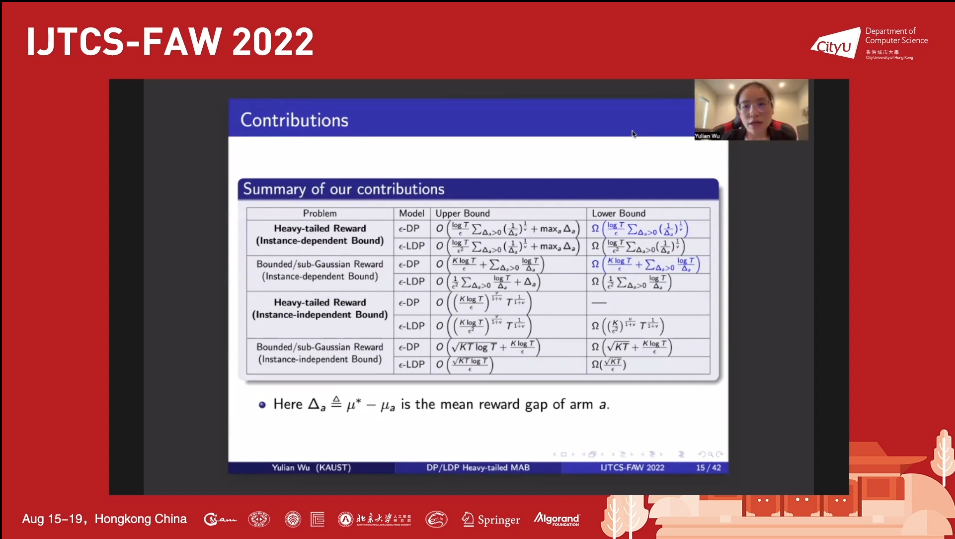
　　最后，为了实现这些（接近）最优率，讲者设计了几个实例和私有鲁棒的估计模型，用来作为理论的支撑。

 

　　

Optimal Private Payoff Manipulation against Commitment in Extensive-form Games

陈昱蓉，北京大学

 

 

　　在扩展式博弈（extensive-form games）中，两个参与者的决策一般是独立（同时）的，当双方信息无隐藏时，子博弈完美均衡得到体现并可以用后向归纳计算。然而，领导者在子博弈完美均衡中不一定可以得到自己想要的结果。如果领导者可以先向追随者告知并承诺自己的决策，这可能改变追随者的策略从而使博弈进行到自己想到的子博弈中。为了利用战略承诺（strategy commitment）这一有用的博弈策略，领导者必须了解关于追随者收益函数的足够信息。然而，这给追随者留下了提供虚假信息并影响最终游戏结果的机会。相较于他如实报告，追随者可能会得到一个对他更有利的结果通过向领导者错误地报告一个精心设计的收益函数。这种博弈同样有着丰富的应用场景，比如电商和顾客之间的博弈等等。

 

 

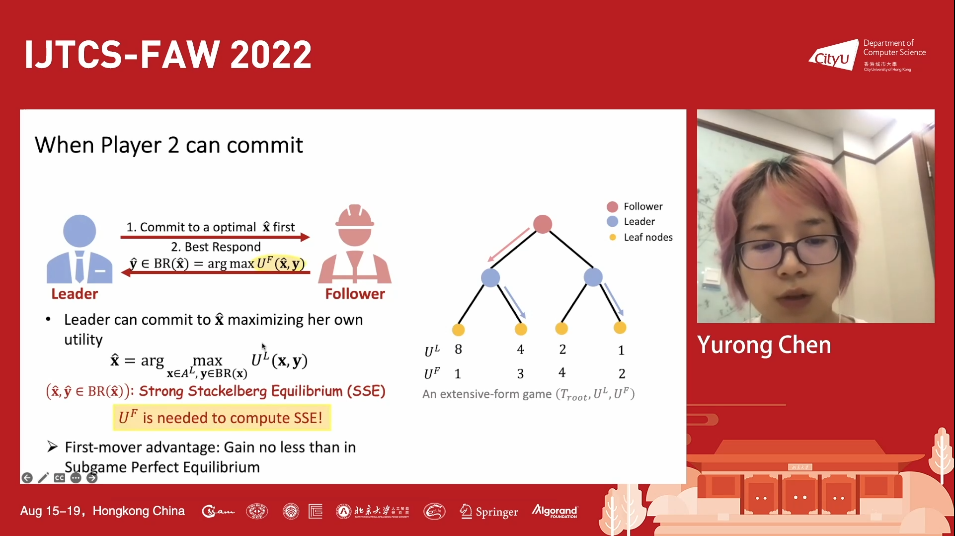
　　基于这个现象，讲者研究了追随者在扩展式博弈中通过这种战略行为进行的最佳操纵。该博弈可以分为两个阶段，追随者向领导者汇报收益函数，之后领导者告知追随者自己的策略。讲者考虑了不同的情况：领导者告知的是纯（pure）策略还是行为（behavioral）策略，前者是确定性策略而后者允许随机化。对于追随者，讲者假设他的最佳回应是纯策略的。讲者还考虑了不同的追随者的需求：设计出只需在所有的均衡结果中存在最大化他的真实效益的收益函数（inducibility），和设计出产生唯一博弈结果的收益函数（strong inducibility）。对于不同的领导者和追随者的设定，讲者都进行了对该博弈的刻画，并针对追随者提供了设计收益函数的多项式算法。因此，讲者的工作完全解决了这个追随者在扩展时博弈上的最优操纵问题。

 

　　

Beyond Characteristic Function Method to Get Exponential Concentration Bound

魏智徳，北京大学

 

 

　　集中界（concentration bound）是指限制了随机变量偏离某个值的概率的不等式。对于独立随机变量来说，通常有两种，一种是切尔诺夫界（Chernoff Bound），另一种是马尔可夫（Markov）/切比雪夫（Chebyshev）不等式。当随机变量复合一些经典特征函数时，我们通常都够通够用已有的不等式去得到指数集中界。然而，讲者指出，即使随机变量只能不符合经典的特征函数，也可以得到指数集中界。通过将尾界（tail bounds）与马尔可夫不等式相结合，讲者展示了随机变量的指数集中界，其密度函数是解析函数的傅里叶变换，这个结果是经典特征函数界无法推导出的。讲者展示了具有平移不变性和解析核的核方法可以在保持接近1的乘法误差内可以将 n 维降到关于 \log n 的多项式的维度，这代表了核方法的近似线性时间近似算法。除了理论介绍之外，讲者给出了丰富的应用场景：在采用核的聚类算法中，新算法可以帮助降维到 \log k 的线性维度中同时保护目标。同样，在线性代数中，讲者也给出了对应的应用。

 

　　

Multiwinner Voting Using Favorite-Candidate Rule

任泽宇，中国人民大学

 

 

　　多胜者选举是在选举问题中备受关注的问题。在讲者研究的问题中，选民和候选人都在一个空间内，每个选民对不同候选人都有不同的偏好，问题的目标是设计一个机制，从候选人中选出能够代表民意的胜者。该问题有着丰富的应用场景，比如公共设施选址，从众多备选设施中选出部分设施建造。讲者采取了每个选民只报告一个候选人的设定，好处在于更加效率，也能保护选民的隐私。当选民的位置是私有的时候，机制设计者的目标变为了如何设计机制去最小化社会成本，同时保证选民报告自己的真实的位置是他们的最佳决策。机制的质量由其失真度来衡量，失真度被定义为机制实现的社会成本与最优成本之间的最坏情况下的比率。

 

 

　　讲者首先给出了一个简单的机制，选出两个得票最多的胜者，但坏处是失真度很大。讲者指出，每两个候选人之间的最大和最小距离的比率在设定中起着至关重要的作用。讲者根据维度来讨论两种情况。当选民和候选人位于一维空间时，讲者建立了几个关于失真度的下界，并且给出了一个新的机制：极端委员（committee-extreme）机制。对于随机机制，讲者提出了委员独立（committee-independent）机制和随机独裁（random dictator）机制，并给出了失真度的上下界。

 

　　

The Power of Multiple Choices in Online Stochastic Matching

束欣凯，香港大学

 

 

　　线上二分匹配最早提出于1990年，和经典二分匹配不同的是，有一半图是线上的，当点到达的时候，与它相关的边会相应给出，之后算法进行匹配，至今为止，该问题的目标多种多样，可以大致分成三个方面，非权重图上的目标，点权重图上的目标，边权重图上的目标。讲者主要研究的是线上随机二分匹配（online stochastic matching），最早提出于2009年。与之前不同的是，线上点改为了线上类，每一个类的邻接边是已知的。线上点到达的时候，会有不同的几率作为不同的线上类，不同类对应着不同的已知边。

 

 

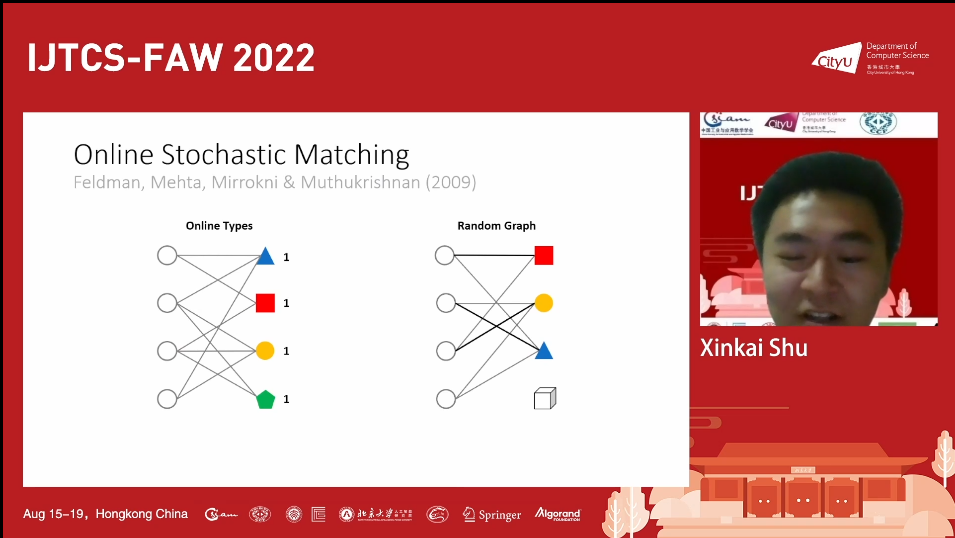
　　在该问题中，算法和最优解的计算和分析是十分困难的，为了方便计算，该问题一般采用能够接近匹配线性规划（LP）的到达比（arrival rate）来衡量算法的表现，越大代表表现越好。作者首先给出了一个简单的随机抽样算法，能够得到 1-1/e 的到达比。在之前的算法中，每个点只考虑两种对于边选择，之后有两个主要的提升方向，增加对边的选择量或者增加 LP 中的约束，每个方向都有一系列的工作。对于增加选择量，最近的成果是每一个到达的点可以从三条边中选择进行匹配的算法。对于整数到达比，目前的工作最高能到0.7299，对于一般到达比最好能到0.711。 讲者考虑了更多选择的情况，相较于之前的工作，增加对边的选择量显然可以得到更高的到达比，但工作难度会增加很多。当泊松 LP 结构时，讲者提出了两种方案，第一种是上半部抽样算法（top half sampling），在对应设定下，到达比从 1-1/e 提到了0.706，第二种是泊松线上对应选择算法（poisson online correlated selection），对于非权重图，到达比从0.711提到了0.716，对于点权重图，到达比从0.700提升到了0.716。