本文为论文 Simulating Virus Diffusion in Networks with Quantum Computers 的解读，探讨了运用量子计算机模拟病毒在复杂网络中传播过程的可能性。运用量子计算机上的哈密顿演化，我们可以模拟经典计算机上难以计算的完全的马尔可夫过程。本工作由北京大学袁骁课题组和中国科学技术大学的研究人员合作完成。

论文地址：https://arxiv.org/abs/2208.11394

01 研究背景

　　模拟病毒在复杂网络中的传播是一个经典问题。研究这类问题可以让我们对病毒传播的趋势进行一定的预判。同时，在生态学中，人们研究一个物种如何与其他物种以及周围环境相互作用；在传播学中，由于广告的传播与病毒的传播行为类似，因此这类问题在市场营销中也有一定的应用。更多的应用都可以视为一种“病毒隐喻”，因此我们的工作将主要围绕病毒在复杂网络中的传播。随着以新冠病毒为代表的流行病日益成为全球公共卫生问题，人们对理解病毒传播过程的需求愈发迫切。

　　传统上，病毒传播过程可视为一个马尔可夫过程。马尔可夫过程通过构造状态转移矩阵来进行离散时间片上的时间演化。但是由于马尔可夫矩阵规模随着模拟格点规模的指数增长，在传统计算机上将无法模拟完全的马尔可夫过程。因此人们不得不进行一些近似，例如在平均场近似下，人们引入了在传播网络上的 SIR 模型。SIR 模型将人群分为几个部分，分别为：易感人群（Susceptible）、感染人群（Infected）和恢复人群（Removed），感染者会感染易感人群，而易感人群在痊愈后变成恢复人群。在此分类的基础上，通过建立微分方程，计算机可以模拟很大规模的病毒传播过程。但是由于平均场近似，这种方法无法考虑网络中存在的涨落，即总有 \left\langle X_{i} X_{j}\right\rangle=\left\langle X_{i}\right\rangle\left\langle X_{j}\right\rangle 。多数情况下，平均场近似是一个很好的近似，在下文中，我们将把我们运用量子计算机模拟完全马尔可夫过程的结果与平均场近似的结果进行比较，发现二者吻合地很好。

02 工作内容

　　在我们的工作中，我们同样将人群分为易感人群、感染人群和恢复人群。我们研究在一个给定传播网络中的社区传播行为，例如图1给出的一个较为简单的社区环境。除此之外，我们考虑感染者是从别处引入的情况，例如由于出差或者旅游来到此地。且我们只关注引入感染者之后很小的一段时间内的传播情况，此时染病者尚未恢复，且在潜伏期内被传染者还没有传播病毒的能力，那么我们无需考虑恢复者 (R=0) 以及染病者进行的二次传播。在 SIR 模型的框架下，此问题变成了一个简单的 SI 模型。根据 SI 模型建立的微分方程，易感人群的总数将出现单指数衰减的行为。我们将在量子计算机的数值模拟中看到相似的行为。

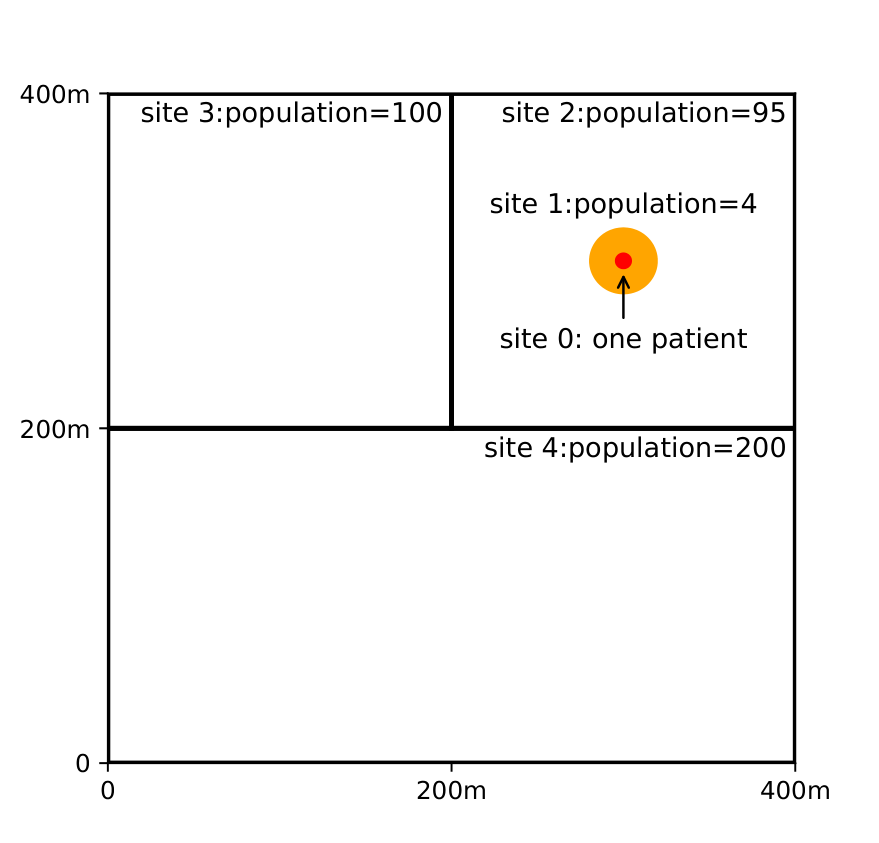
图1：一个给定的社区环境，图中的每个长方形代表一个社区，红点代表我们引入的一个病人，橘色的圆代表病人的家人。此网络一共有5个位点，每个位点的人口数已在图中标明。

　　在我们的模拟中，我们构造了一个有效哈密顿量，并通过哈密顿量的薛定谔演化来计算病毒在复杂网络中的传播行为。由于病毒传播过程与经典热力学传播过程的相似性，哈密顿量的构造借鉴了人们对量子热动力学的认识。我们将量子系统分为规模相同的两部分：热库（bath）和系统（system）。热库和系统采用同样形式的类似于经典 Ising 模型的哈密顿量，且二者之间存在一个较小的相互作用。具体的哈密顿量形式可见原文章。由此我们就可以模拟一个给定温度下的系统的热扩散过程。在我们的模拟中，我们将热库维持在基态，即绝对零度下的热态。根据量子热动力学的结论，系统（system）在经历无穷长时间后也将达到绝对零度，从而达到系统的基态。此基态对应于所有人都感染的状态。现实中，由于感染者在短时间内将持续处于染病状态，在我们的数值模拟中，每隔一段时间我们就会将病人代表的量子比特重置为染病态（染病态用例如计算基下的 |1\rangle 来表示）。

　　通过上述有效哈密顿量进行的薛定谔演化，我们得到了类似经典 SI 模型的易感人群 (S) 的单指数衰减行为（见图2）。通过对有效哈密顿量进行的微扰论分析，我们找到了哈密顿演化对应的马尔可夫状态转移矩阵，并且得到了指数衰减因子的解析表达式。

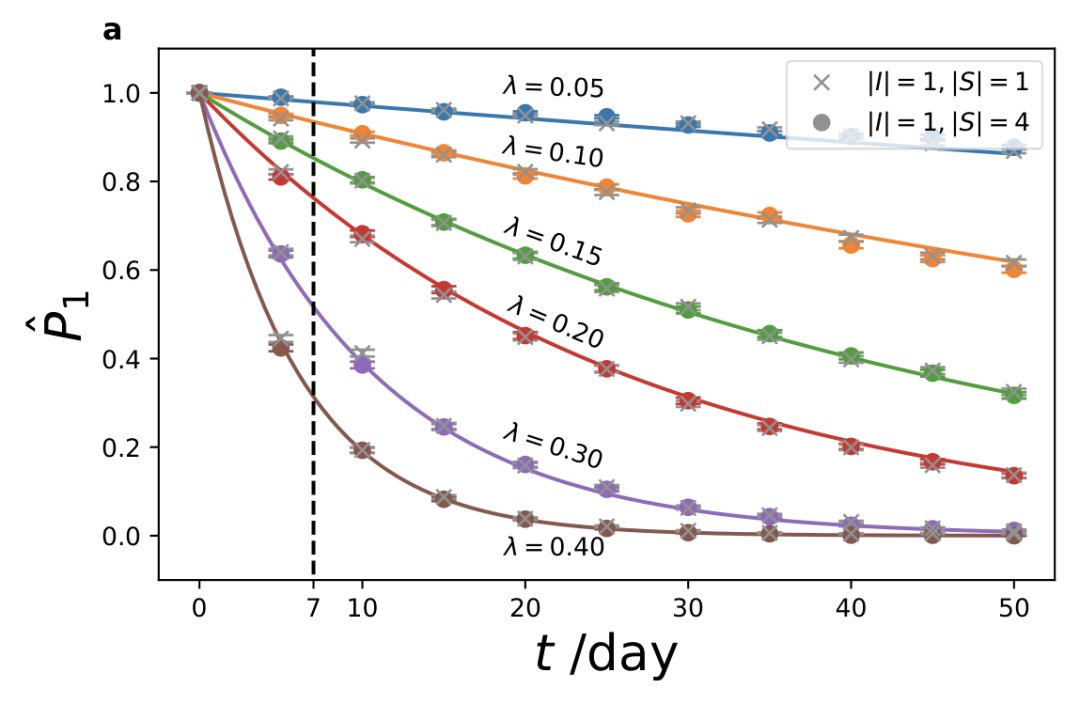
图2：只考虑一个感染者位点和一个易感人群位点（系统和热浴共4个 qubits，图中用“x”表示）以及4个易感人群位点（系统和热浴共10 个qubits，图中用圆圈表示）时的未感染率与时间的关系。所有的时间演化曲线呈单指数衰减行为。不同曲线代表了不同的耦合强度，代表病人与易感人群的平均接触数。

　　有效哈密顿量存在一些未定参数，这些未定参数需要通过病毒学的调查数据作为输入。在我们的工作中，我们给出了系统的确定哈密顿量未定参数的具体方案。作为一个简单的示例，我们运用了流行病学中比较容易获得的基本再生数（Basic reproduction number）和家庭继发率（Secondary attack rate）作为确定哈密顿参数的输入，模拟的对象为2021年末出现的新冠病毒变种奥密克戎（Omicron）。结合之前提到的指数衰减因子的具体表达式，通过调节哈密顿量的未定参数，我们就可以使哈密顿模拟的结果与奥密克戎的基本再生数和家庭继发率相吻合。由此，我们可以针对更复杂的情况进行预测。

　　作为一个例子，我们运用上述确定的哈密顿量参数模拟了在图1所示的社区环境中引入一个病人和两个病人时的病毒传播过程，结果如图3所示。我们看到，相比于引入一个病人，引入两个病人时各个社区平均每个人的感染概率有明显的提高。

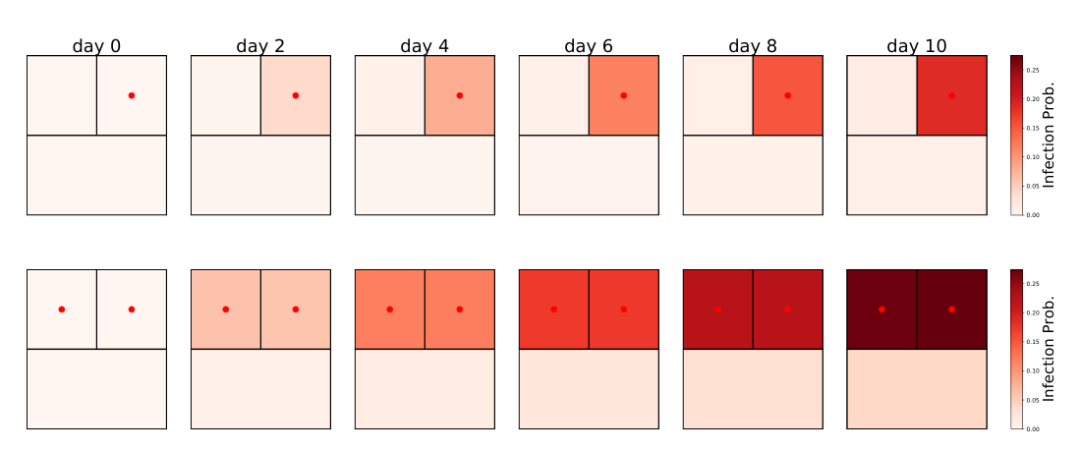
图3：数值模拟结果。红点代表了感染者的位置，每个长方形代表一个社区。从左到右分别是演化的不同时间，不同颜色深度标记了感染率。

03 讨论与展望

　　本工作展示了运用量子计算机模拟复杂病毒传播过程的可能性。运用量子计算机的优势，我们可以模拟一个完全的马尔克夫过程。本工作中所有的模拟是在经典计算机上完成的，更大规模复杂网络上的病毒传播过程有望在未来的大规模量子计算机上实现。但是本工作使用的有效哈密顿量仍十分简单，在接下来的工作中，通过对有效哈密顿量进行修改，我们或许可以模拟流行病学中更多的过程，例如二次传播，以及病人的免疫，死亡，免疫丧失等等。此外，哈密顿量中的未定参数需要更多来自流行病学的输入，例如各个位点之间的平均接触数。运用更多的流行病参数作为输入来确定哈密顿量将使得哈密顿模拟得到的结果更加可靠，也是我们下一步可能的工作方向。