第三届国际理论计算机联合大会（International Joint Conference on Theoretical Computer Science-Frontier of Algorithmic Wisdom，IJTCS-FAW）由北京大学讲席教授邓小铁于2020年牵头发起，第三届于2022年8月15日-19日线上线下交互举行。大会由中国计算机学会（CCF）、国际计算机学会中国委员会（ACM China Council）、中国工业与应用数学学会（CSIAM）联合主办，香港城市大学（CityU）承办，北京大学前沿计算研究中心、北京大学人工智能研究院协办。

　　

　　8月19日，大会女性论坛如期举行，由上海纽约大学郭斯瑶助理教授、中国科学院计算技术研究所张家琳研究员主持。小编为大家带来论坛精彩回顾。

 

 

报告精彩回顾

 

Quantum Copy Protection and Unclonable Cryptography

刘家惠，德克萨斯州大学奥斯汀分校

 

 

　　量子信息的不可克隆性已被应用于量子密码学。1963年，Wiesner 提出了量子货币的开创性思想：用量子态编码出货币，而这些货币由于量子力学的原因无法被伪造。这个想法后来被用于著名的 BB84量子密钥分发（QKD）协议。

　　

　　在本次演讲中，讲者介绍了不可克隆量子态在信息论结构（如 Wiesner 量子货币和 QKD）之外的应用：我们使用和改进了一些过去的量子货币工具，并结合经典密码学的技术来实现更多的不可克隆态。其中，讲者重点介绍了两个应用——量子复制保护（quantum copy protection）和不可克隆的密码学（unclonable cryptography）。

　　

　　其中一个应用是量子复制保护（quantum copy protection），由 Aaronson 在2009年首次提出。对于经典软件程序，恶意用户只要购买一份软件就可以将其复制分发。Aaronson 指出，我们可以将经典函数编码为量子态，运行量子态的函数能得到与经典函数相同的输出，但同时保护了函数不能被复制为两个。讲者的工作解决了 Aaronson 提出的一个开放性问题，即是否可以为任意不可学习函数建立一个相对于 classical Oracle 的量子复制保护方案。讲者介绍了构造方法和简要证明。

　　

　　更进一步的问题是能否仅使用密码学假设代替 classical oracle 进行构造，但已有工作证明了一般情况下的不可能性。讲者对此提出了可能的解决方案，在适当减弱安全性条件、以及限定特定的函数类别（包括Signature、Decryption、PRF）的条件下给出了构造方法。

 

 

　　讲者表示，一方面量子计算机威胁了传统密码学的安全。另一方面，我们也意识到量子信息有许多特性，这也将赋予密码学新的能力，可以基于量子信息构建多种密码学工具。

 

　　

Hardness Results for Weaver's Discrepancy Problem

张鹏，罗格斯大学

 

　　张鹏教授向我们展示了与耶鲁大学的丹尼尔·斯皮尔曼（Daniel Spielman）合作的 Weaver 差异问题（Weaver's Discrepancy）的研究结果——如何将 n 个物品划分为两组，让两个组是互相相似的，换句话说让两组的差异较小。

　　

　　张教授表示，这类研究问题可以应用于两个方向。第一个应用与设计随机对照试验（也称为 AB 测试）有关，研究者将被试人分成实验组与对照组，并希望两个组是相似的。随机对照试验已被广泛用于测试医学、教育、政治学或计算机科学以及其他一些领域中的新疗法或新干预措施的有效性。第二个应用与稀疏化有关。还有更多其他应用程序用于差异问题，比如数值积分运行理论、伪随机性、通信复杂性等。

 

 

　　张教授的工作研究了 Weaver 差异的计算困难性。首先，她向大家介绍了对于个维向量的一个划分，Weaver 差异的定义。而一组向量的 Weaver 差异定义为所有划分取得的 Weaver 差异的最小值。为了让 Weaver 差异有意义，假定输入向量满足 isotropic position 和 small vectors 条件，称为 α- Weaver 向量。

 

 

　　张教授提出问题：如何对这些向量进行划分，以将 Weaver 差异最小化？随机划分的 Weaver 差异是 O(√αlogd) ，为了得到非平凡的结果要求 α 随着维数 d 增大而减小。但 Marcus、Spielman 和 Srivastava 在2015年证明了总是存在不超过 √8α +2α 的划分方案，解决了 Kadison-Singer 问题。然而，他们的证明只是一个存在证明，目前还不清楚是否可以在多项式时间内计算出这样的划分。

　　

　　关于 Weaver 差异的计算困难性，张教授引入了两个相关的问题。第一个问题是是否能在多项式时间内找到划分方案使 Weaver 差异不超过 O(√α) 。第二个问题是若已知一组 α-Weaver 向量存在 Weaver 差异为0的划分，是否能在多项式时间内找到差异远小于 √α 的划分方案。第一个问题的答案暂时是未知的，而张教授的工作解决了第二个问题，给出了两个较强的困难性结论。

 

 

　　张教授指出 Weaver 差异问题和集合拆分问题之间存在一些联系，并描述了如何将集合拆分问题规约到 Weaver 差异问题。对一个集合拆分问题，先将每个元素对应到一个对角矩阵，再将对角矩阵分解为 Weaver 向量，就得到了一组 ¼-Weaver 向量，并且可以验证当集合可拆分时这组向量的 Weaver 差异为0，当集合不可拆分时这组向量的 Weaver 差异至少为 ¼ 。由此完成了集合拆分问题到 Weaver 差异问题的规约，证明了 Weaver 差异问题的 NP 困难性。

 

　　

Graph Limits and Graph Homomorphism Inequalities

韦帆，普林斯顿大学

 

 

　　最近发展起来的图极限理论是一个有力的数学工具，可以从连续的视角研究图论问题。在本次演讲中，韦帆教授展示了图极限理论如何帮助解决图同态不等式，以及如何作为一个有用的工具在极限组合学领域帮助学者们取得进展。

　　

　　韦教授首先介绍了 graphon 和 kernel 作为图极限的一种描述方式，并引出了图同态密度不等式。韦教授证明了一个图同态密度不等式是否对任意 kernel 成立是一个不可判定问题。这意味着没有一种系统的方式能对任何成立的图同态密度不等式给出证明。一个推论是存在图同态密度不等式对任意 kernel 都成立但却无法写成平方和的形式。

　　

　　韦教授接着介绍了 Ramsey Multiplicity Question，并介绍了两个具有挑战性的开放问题：Sidorenko 猜想和任意染色数的 common graph 的存在性，并介绍了关于这两个猜想取得的进展。

 

　　

A Faster Interior-Point Method for Sum-of-Squares Optimization

姜舜华，哥伦比亚大学

 

 

　　讲者介绍了她和 Bento Natura、Omri Weinstein 在 ICALP'22的最新结果，提出了一种用于平方和优化的内点方法，达到了多项式级别的速度提升。此算法的核心是一个动态数据结构，用于在多项式插值基下保持 SOS 障碍函数的 Hessian 逆。

　　

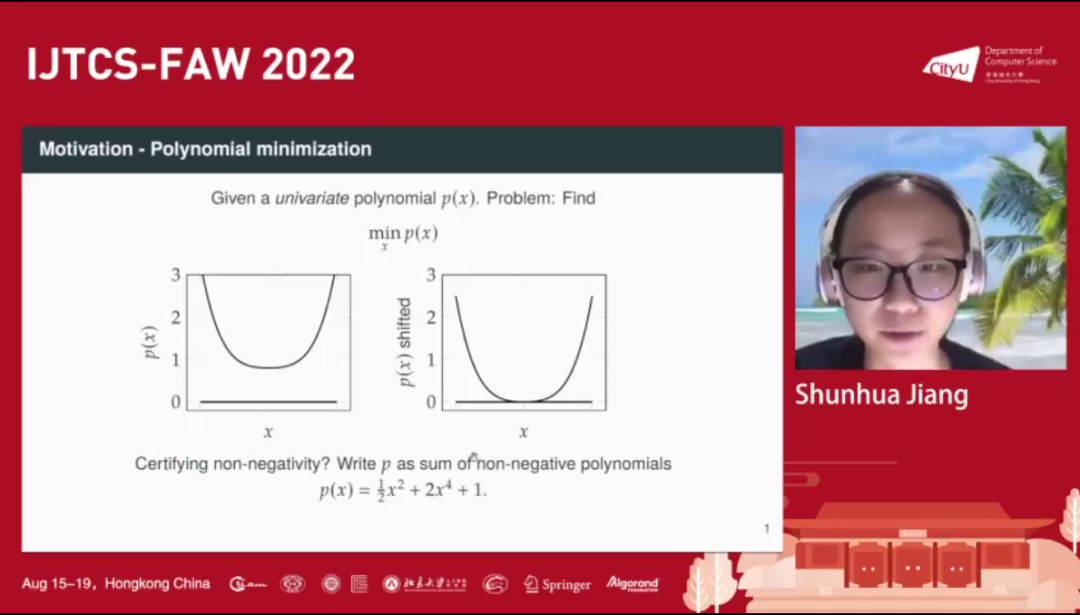
　　讲者首先介绍了研究问题的背景。在多项式最小化问题中，目标是找到一个单变量多项式函数的最小值。这个问题可以等价于检查这个多项式减去一个常数之后是否是非负的。

　　

　　讲者指出，为了证明多项式的非负性，最简单的方法是将它写成若干个多项式的平方之和的形式。这样的形式被称为 SOS（sum of squares）。对于多变量多项式，存在非负多项式并不能写成平方和的形式，但随着度数 d 不断增加，最终趋近于无穷大时，结果将会是精确的。而如果 d 被限制在较小的数字，则只能获得一个近似。

 

 

　　接下来，讲者引入了 SOS 优化（Sum-of-squares optimization）问题。它可以看作一个锥规划问题，想要最小化一个线性目标函数，并且 x 被约束为 SOS 多项式。

　　

　　讲者还介绍了圆锥规划和现有算法的一些背景知识。讲者介绍了内部点方法的概要，在目标函数中加入一个障碍函数（barrier function），通过不断迭代找到目标函数的下一个最小化结果，最终达到一个较为精确的近似值。Nesterov 和 Nevirovskii 提出了关于内部点方法的迭代次数的理论。

　　

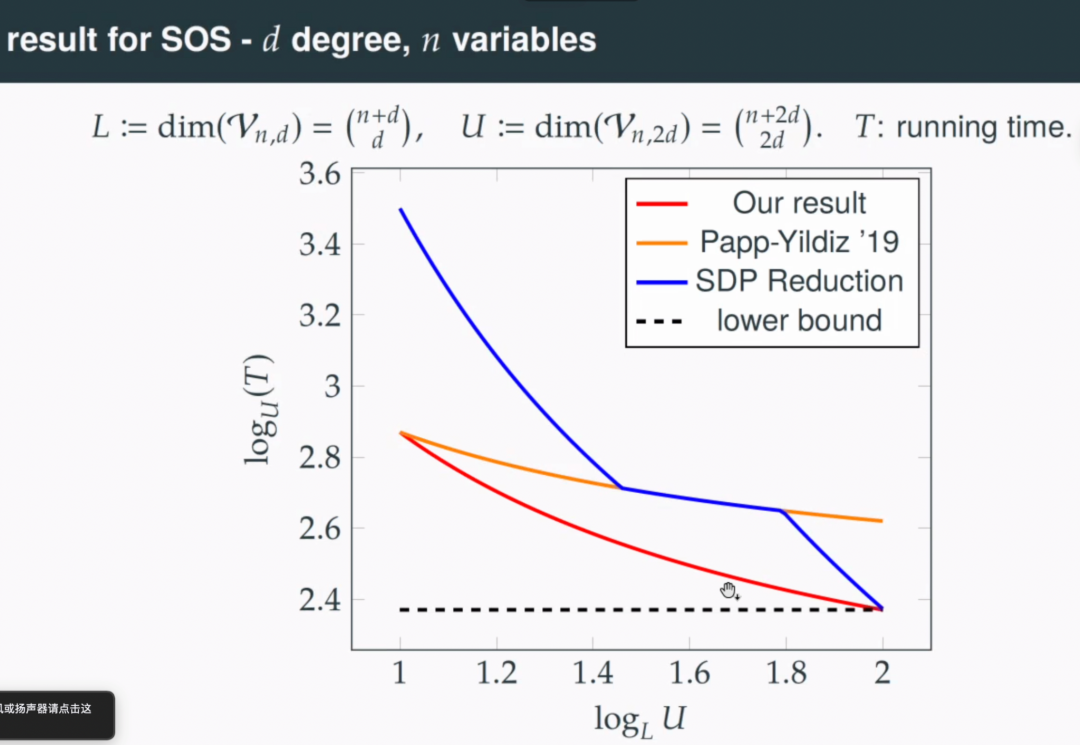
　　讲者介绍，利用对偶 SOS 问题和 Nesterov 提出的理论，可以将 SOS 优化问题归结为更难的 SDP（Semi-definite programming）问题然后求解。但这一做法会将变量数从增加至 L^2 。另一种方法是为 SOS 问题定义一个直接障碍函数。Papp-Yildiz 通过使用插值多项式作为基底，使线性算子可以高效地计算，得到了复杂度为 O(L^0.5 ·U^w) 的算法。

　　

　　最后讲者介绍了自己提出的算法。讲者使用的主要技术是动态地维护 Hessian 矩阵的逆，只进行低秩更新，降低每次迭代的时间复杂度。提出的算法在复杂度上优于 Papp-Yildiz 和 SDP reduction，表明这一方法成为目前最快速最先进的算法。

 

　　

圆桌讨论精彩回顾

 

理论计算机和数学领域一些女性学者在海外求学生活的分享

　　

 

　　作为女性论坛的特色环节，圆桌讨论由中国科学院计算技术研究所张家琳研究员和上海纽约大学郭斯瑶助理教授主持，参与讨论的四位女性嘉宾即为女性学者论坛的四位讲者，另外还邀请了上海财经大学陆品燕教授作为特别嘉宾。

 

　　Q：最初的时候是怎么和这个理论计算机或者是数学领域结缘的？

　　张鹏：高中的时候通过数学竞赛培养了对数学的兴趣。本科时参加了应用运筹学，了解了线性规划和组合优化的问题。参加了一个有关近似算法的 reading group，氛围非常好。然后我就开始慢慢的学习了 TCS。　　

　　姜舜华：从本科开始就想做科研。我本科是在清华姚班，姚班本来的这个培养计划里面理论的课比较多。本科的时候有过一些科研的经历，接触了一些深度学习的内容。后来去丹麦交换了一个学习，跟着丹麦的老师做 TCS 的 project。　　

　　韦帆：高中的时候通过数学竞赛培养了对数学的兴趣。本科时参加了 abstract algebra 和 real analysis 两门课，觉得理论很有趣。在本科时花了一学期做出了教授给的一个代数组合的难题，收获了成就感和对科研的热情。　

　　陆品燕：第一次感受到理论计算机的魅力是完整听下并吸收一篇讲座时。第一次做科研是本科毕设。这些初期的经历支持着我继续之后的学术生涯。

　　

　　Q：在真正投入理论计算机领域一段时间之后，有没有发现一些和最初入门时对这个领域的最初印象不同的地方？

　　韦帆：本科刚开始做科研时，发现出结果还挺快挺容易的。但是其实到后面真正开始读 PhD 的时候，科研其实是挺难的，感觉99%的时间其实是一点思路都没有。包括 PhD 后期开始接触教职，也要去考虑不同类型的学生适合什么题目，什么题目适合组队做。

　　姜舜华：读博的时候经常好几天不知道自己到底有没有 make progress，经常可能陷入一种焦虑抑郁的情绪。找到一个内心释放的点，以及每天都给予自己一些正向的反馈，都是很有用很重要的缓解压力方式。　　

　　张鹏：从刚接触理论计算机到现在成为教职，我的一点变化发生在选科研题目上。最早我比较关注于问题的技术挑战性，因为我经常被其中的理性魅力所吸引。但现在我会更关注于一些有意思的应用。

　　

　　Q：理论 vs 应用，我们在选择科研方向时应该关注谁？

　　陆品燕：年龄的差异会体现在选题的不同。年轻时追求的更多是解出题目的成就感，后来有了自己比较规律的论文发表计划表，就不会太狂热地追求热点。再年长一些，可能会萌生一个困惑，虽然 TCS 推动了很多领域的进步，但其本身的性质还是颇像一个抽象的智力游戏，现实应用性不高。经过对产业界的观察，我现在认为 TCS 一方面是非常抽象非常基础的纯理论研究，一方面是和现实应用息息相关的研究。目前我更倾向于将 TCS 研究偏向应用性一些。　　

　　刘家惠：理论计算机最开始都是从一个很基础的问题出发的，不断衍生出新的问题。后面衍生出的新问题可能就会变得不那么接地气了。我本身做密码学的研究也会经常陷入这个困惑。但我依旧认为要去尝试将自己研究出来的东西和现实应用联系在一起。不过做纯理论研究如果能够收获满足感和愉悦感其实也不错。

　　

　　Q：你做科研的动力是什么？享受理论本身的美感，享受抢先做出结果的智力竞争，还是因为享受学术社群的合作氛围。男女科研者是否会有不同的答案？

　　姜舜华：第一点的占比可能最大。第二点对我完全不受用，因为如果每天想着要和别人竞争，我的压力会非常大，很大程度上影响我的发挥。我想要补充一点，科研最终极的目的还是要为人类社会服务，自己的研究最终被用于现实社会是我做科研的动机之一。　　

　　刘家惠：一开始是享受理论问题本身，后来是被学术社群的氛围所吸引。在社群中，大家互相给予对方精神和学术支持，所以后来也就慢慢地融入到了科研领域。竞争完全不能够成为我的动力，因为我如果处于一个竞争的环境，总会想着这个问题一定要赶在别人前面做出来，就会压力很大。　　

　　韦帆：第一点能占到70%，第二点可能占到10%。剩下的20%来源于科研带来的生活安排的灵活度和自由度。　　

　　张鹏：对理论的兴趣是我最大的动力。理论研究中经常发现违反直觉的结果。我很享受不断修正自己对问题的认知的过程。　　

　　陆品燕：不同年龄段、不同的性别都会影响这三个导向的占比。

　　

　　Q：在学术领域 being aggressive 是否是好事？女性科研者是否会相对不那么 aggressive？

　　陆品燕：不一定是好事，需要找到一个平衡点。不同的人在不同阶段会有不同。例如在刚进入学术界的阶段，结果导向的想法可能让一个人很快在高水平期刊会议上发表文章，对于自信心的培养和获取学术界认可等等各方面的确是有帮助的，不是完全负面的。但长期来看兴趣驱动是比结果导向更好一些的。　　

　　张家琳：Being aggressive 可能从某种意义上来讲可以为你争取到一些学术资源。但从长期的角度以及动机上来看可能会产生负面的影响。确实有些人在选题时是结果导向为主的，会更多考虑做出的结果能发什么等级的会议。　　

　　郭斯瑶：太具有倾略性的学术氛围是不利于有效合作的。　　

　　姜舜华：从本科经历来看，女性科研者确实会相对不那么 aggressive，可能受小时候的文化教育影响。但有时候学术界还是一个竞技场。

　　

　　Q：女性这样一个身份吧，在大家的求学，工作，生活中有没有带来过一些困扰？

　　姜舜华：女性科研者主要有两个困惑。第一个就是刚刚提到的可能在学术竞技场上不够具有侵略性。第二个则是一个有生育计划的女性可能很难平衡学术工作和孩子。　　

　　张家琳（回应姜舜华）：女性面临的这个困惑和职业选择关系不是很大，相对来讲，做学术已经是在所有职业里面对生育比较友好的一个选项了。尤其是当你选择教职，你的时间会变得相对自由。虽然生育不会使得你被学术界踢出，但可能会使得你无法成为一个学术明星，毕竟孩子和家庭使你没有办法毫无顾忌的在外面奔波。孩子其实带给你生活的影响，不都是负面的，他也会带给你很多不一样的体验。我觉得这一点上，母亲跟父亲的体验是不一样的，尤其在小孩很小的时候，可能母亲能够体验到的成就感会更多更真实一些。　

　　张鹏：我刚到美国时，发现我们学校30个 PhD 学生里只有2个女生。有时候会觉得孤独，因为选择在计算机和数学领域学习的女性很少。

　　张家琳（回应张鹏）：国内的 TCS 圈也同样遇到这个问题。这不仅仅给女性带来了困扰，其实对这个圈内的男生可能也是有一定困扰的。因为从小接触的群体都是男女比例比较悬殊的，所以不太懂得如何和异性去交流。

　　

　　Q：女生也会因为跟男生的交流比较少而导致可能在科研领域占劣势吗？

　　姜舜华：个人认为是会有一些影响的。很多时候新的 idea 和新的 topic 是你在朋友之间交流中产生的，有可能是一起喝酒的时候，有可能是睡觉前。性别差异可能会成为学术交流的壁垒。　　

　　韦帆：我也认为这个现象存在。比如在线下会议的时候，男生往往晚上会一起约着去喝酒，会交流很多想法和信息。而作为女性，我往往不会加入，导致失去这样的交流机会。　　

　　郭斯瑶：的确在男性比例较大的学术社群中，女性身份会增加融入的难度。类似地华人身份也造成需要更多努力去融入社交群体。我认为一个可行的方案可能是形成更多女性的社交群体。　　

　　程郁琨：我们组织了一些女性工作委员会，比如中国工业运用与数学学会设立了女性委员会。每年我们大概都会组织2-3场活动，比如说女性青年教师提升计划。这个计划致力于帮助刚毕业的女性青年教师去快速适应教职工作岗位。主要的活动形式有导师和青年老师相互结对，通过交流一些科研，生活，工作方面的经验，给予青年女教师一些未来的方向。

　　

寄   语

 

　　姜舜华：希望每个女生，包括我自己可以更好的相信自己，并且更勇敢的为自己争取吧。　　

　　张鹏：希望大家能享受科研，然后也享受生活。　　

　　韦帆：希望大家能吃好睡好，工作好。　　

　　刘家惠：希望大家都能吃好睡好，做自己觉得有用且有趣的事情。虽然大家都还是平凡人，但只要不成为大家自己心里觉得平庸的人就好。　　

　　陆品燕：我觉得对年轻的学者，特别是女性学生来说，希望大家自信一点，科研是非常适合女性学者的！