第三届国际理论计算机联合大会（International Joint Conference on Theoretical Computer Science-Frontier of Algorithmic Wisdom，IJTCS-FAW）由北京大学讲席教授邓小铁于2020年牵头发起，第三届于2022年8月15日-19日线上线下交互举行。大会由中国计算机学会（CCF）、国际计算机学会中国委员会（ACM China Council）、中国工业与应用数学学会（CSIAM）联合主办，香港城市大学（CityU）承办，北京大学前沿计算研究中心、北京大学人工智能研究院协办。

　　8月15日下午，大会“量子计算”分论坛如期举行，中国科学院计算技术研究所张家琳研究员主持。小编为大家带来论坛精彩回顾。

Optimal Quantum Circuit Constructions for Quantum State Preparation and General Unitary Synthesis

张胜誉，腾讯量子实验室

　　本报告主要关注量子计算中三类基本问题：

• 　量子态制备（QSP）：给定一个复向量，如何制备一个以该向量为振幅的量子态。
• 　量子随机访问存储器（QRAM）：给定一个索引，如何获取索引所对应的量子态，这一问题可以被看作条件 QSP（CQSP）问题。
• 　通用酉算符综合（GUS）：给定一个酉算符，如何使用基本的量子电路去实现该算符。

　　报告关注的是，给定一些辅助量子比特，实现上述三个问题的量子电路最坏情况复杂度是什么样的。从直觉上来说，辅助比特越多，所需要的电路深度就越浅，这反映了用空间换时间的思想。报告人的工作给了 n-QSP、QRAM（或 (k,n)-CQSP）和给出了小规模辅助比特下 n-US 的电路深度复杂度的渐近紧界。报告人的工作还改进了大规模辅助比特下 n-US 的电路深度复杂度渐近上界，然而这一界和已知的深度下界依然有一个指数的距离，如何将这样的距离缩小是一个有趣的问题。

　　报告人还简单介绍了处理这类问题的主要技术。过去处理 QSP 问题的框架主要是 Grover-Rudolph 框架，思路非常直观，就是一比特一比特、一分支一分支地做单比特旋转，逐比特地利用越来越大的全域控制门（UCG）来实现 QSP。另一种方法是最近 Keneridis 提出的，如果允许用一个长为 2^n的 1 进制编码去表示，那么相应的 QSP 变体问题有线性深度的电路。这两种方法都不能得到有效的 QSP 方案，报告人介绍了如何利用辅助比特，或者在无辅助比特的情况下利用自身空间，结合多种报告人新发展出的复杂技术，来实现门操作的大量并行化，从而降低电路深度，最终到达理论最优值。

Quantum Adiabatic Theorem Revisited

段润尧，百度研究院量子计算研究所

　　本报告介绍了在量子计算中广泛应用的量子绝热定理，回顾了其发展历史，并给出了此定理的一个简单的证明。

　　报告首先从量子力学中的薛定谔方程引入量子绝热定理，接着介绍了过去关于量子绝热定理的研究。该定理表明：对于一个随时间演化的哈密顿量，系统在 T=0 时刻处于 H(0) 的本征基态，如果系统的演化速度足够慢，并且时间 T 足够长，那么系统在 T 时间的量子态将被保持在接近 H(T) 的基态。其中时间T应满足大于等于一个由最终态误差、哈密顿量能隙和哈密顿量演化一阶、二阶导数的范数所决定的多项式。

　　报告首先介绍了本征值为0的特殊情况下的定理及其证明。证明的关键在于以下三点：将演化分解为 Dyson operator 并引入后者的一个微分关系；最终本征态和实际量子态之差的简洁积分表示；操作上述表达式，创造一个 1/T 的系数。报告对上述三点进行了简单的证明，从而得到了误差 Õ(1/T) 的结论，并通过范数不等式估计了误差常数的上界，从而得到最终结论。此外，报告指出，将哈密顿量减去不为0的本征值可以将情况推广至更一般的定理证明。

　　此外，报告还介绍了量子绝热定理在量子近似优化算法中，来完成从某个哈密顿量到另一个未知哈密顿量基态的演化，以及其在单量子比特态制备上的应用。最后，该证明与之前的工作相比，所获得演化时间估计优于之前相应文献中由 Ambainis 和 Regev 所给出的界，同时证明更加简洁，不需要引入绝热演化和复分析相关的概念。

Winning Mastermind Overwhelmingly on Quantum Computers

李绿周，中山大学

　　报告主要介绍了着眼于珠机妙算（Mastermind）游戏的量子策略，得到了该游戏量子复杂性的完整刻画，并构造了最优的适应性和非适应性量子算法。

　　Mastermind 游戏是一个两方游戏，包括编码者和解码者，编码者秘密地选择一个 n 位的 k 进制串 s ，解码者希望通过与编码者尽可能少地问答之后获得这个秘密串 s 。在每轮问答中，解码者可以猜测一个串 x 发给编码者，然后编码者反馈 B(s,x) 和 W(s,x) 给解码者，其中 B(s,x) 表示 s 和 x 有多少个位置的字符是相同的，称为黑钉查询；W(s,x)  表示 s 和 x 有多少个字符相同但是位置错误，称为白钉查询。关于 Mastermind 游戏的算法研究就是要为解码者设计一个策略，使得其使用尽可能少的问答次数而获得秘密串 s。问答的次数称为查询复杂度。报告指出，Mastermind 不仅作为一个流行游戏得到了大众的关注，而且作为一个科学问题得到了学术界的深入研究，它和信息论以及图论等数学及计算机领域有密切关系。

　　相应算法可以分为适应性与非适应性：在适应性算法中，查询是一个接一个地进行的，下一个查询可能取决于之前的查询和答案；而在非适应性算中，查询必须一次性并行提供。报告介绍了主讲人所在课题组最近在 Mastermind 游戏的量子策略方面的成果，给出了适应性和非适应性场景下的量子复杂度性和最优量子算法。对于非适应性情况，Mastermind 的量子复杂性为 Θ(k) ，并构造了最佳的非自适应精确量子算法，消耗 k-1 次黑钉查询；对于适应性场景，Mastermind 的量子复杂性为 Θ(√k) ，并构造了最佳的自适应精确量子算法，消耗 O(√k) 次黑钉查询。

　　报告最后指出，非自适应算法比自适应算法更实用，因为前者只需要运行一个更短的量子电路 Θ(k) 次，而后者需要运行一个由  Θ(√k) 个模块组成的更长的量子电路。

Numerical Framework for Finite-size Security of Quantum Cryptography

周泓伊，中科院计算所

　　本报告关注量子密码学中的两个主要问题，量子密钥分发（QKD）和量子随机数生成（QRNG）。量子密钥分发就是利用量子计算的技术解决密钥分发的问题，经典的协议有 BB84，利用量子态来做容错编码。理论的主要任务是分析 QKD 协议的安全性，有基于熵的方法和基于相位误差的方法。证明安全性的工具主要有分析法和数值法，数值法不依赖协议的具体结构，是本报告主要的方法。另一方面，量子随机数生成依赖于量子态振幅的波恩解释：量子态振幅的模平方是该态出现的概率，利用量子力学的随机是真随机。一般来说 QRNG 的高效率和高安全性是冲突的，从高效率到高安全性有各式各样的 QRNG，本报告关注的是半设备无关的 QRNG（semi-DI QRNG），即随机数的发生源和接受处至少有一个是可信任的。报告的目标是证明有限轮试验的情况下（有限规模），在有协同攻击（coherent attack）下的 QKD 和 QRNG 的安全性。

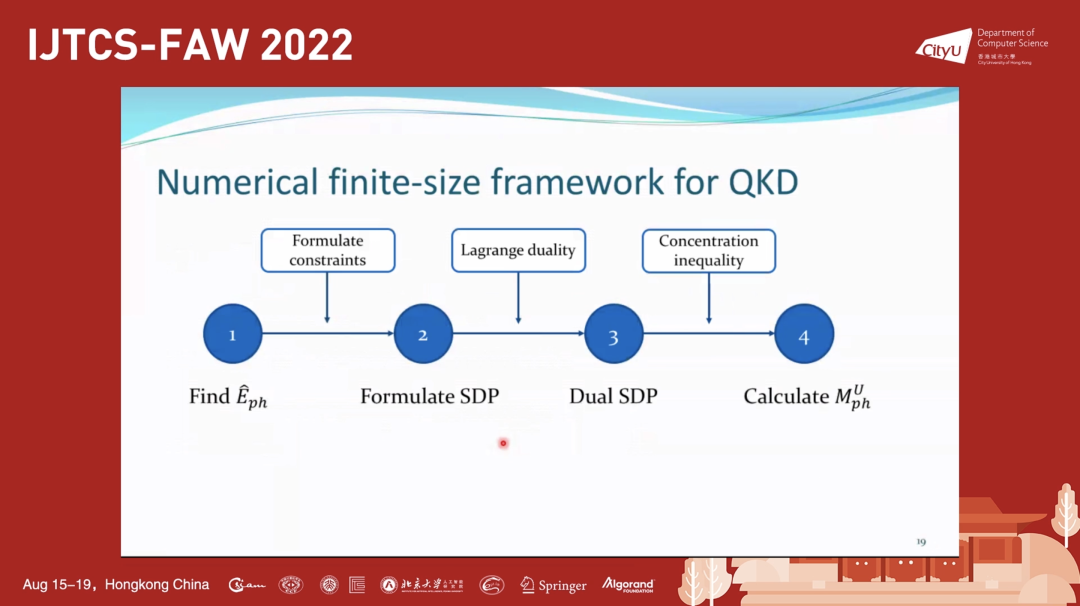
　　报告提出了一种分析 QKD 安全性的有限规模数值理论框架。第一步，将一个真实的 QKD 协议等价于一个基于纠缠的协议，然后得到一个相位误差算符。第二步，利用相位误差算符将问题写为一个半正定规划（SDP），这是一种特殊的凸优化。第三步，用标准的 Lagrange 对偶写出对偶 SDP。为了处理有限规模效应和一般的攻击，报告人的工作使用了集中不等式并将相位误差率换为相位误差数。报告举了一个例子用以说明这一框架，即简化后的相位匹配 QKD（phase-matching QKD）。

　　类似地，报告给出了 QRNG 分析的有限规模数值理论框架。与 QKD 最大的不同是，这里由 SDP 所决定的量是猜测概率。同样，报告给了一个运用该框架的例子，即时间间隔相位编码 QRNG（time-bin phase-encoding QRNG）。