本文是第三十五届人工智能大会（AAAI 2021）入选论文《On the Approximation of Nash Equilibria in Sparse Win-Lose Multi-player Games》的解读。

　　Polymatrix Game 是一类重要的多人博弈模型。这一模型最主要的特点是能拆成多对双人博弈，如下图所示。每人的收益为所有他参与的二人博弈的收益和。另外值得强调的一点是每人在所有的二人博弈中都只能使用同一个策略。整个游戏可以用一个  的收益矩阵表示下来。

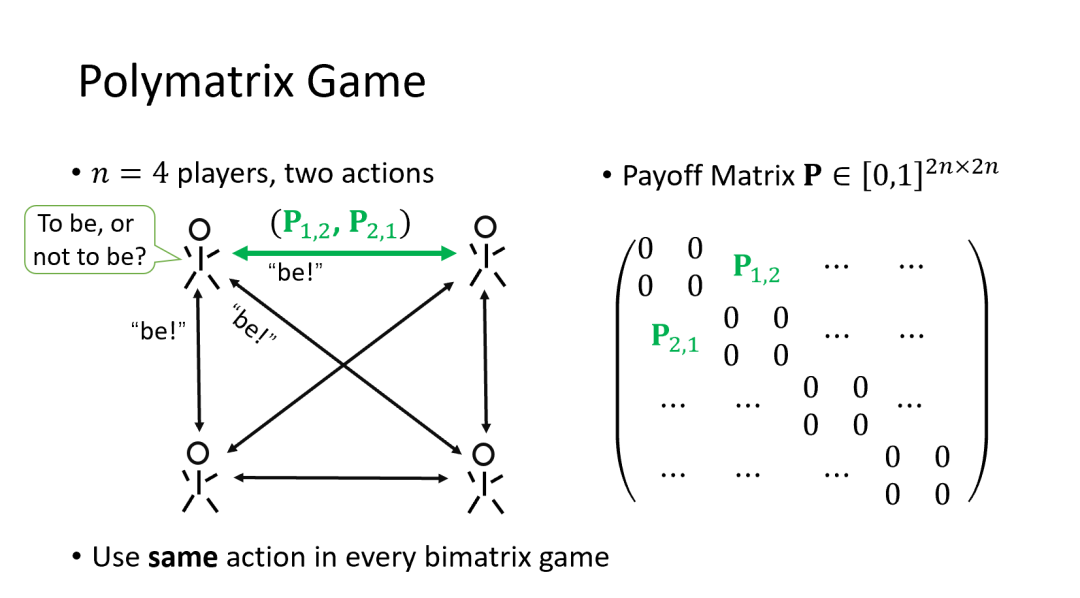
　　本文研究了纳什均衡计算在一类非常特殊的 Polymatrix Game 下的计算复杂度。我们定义了-Sparse Win-Lose Polymatrix Game (SWLP)，其中：

•  -Sparse 表示收益矩阵每行最多有  个非零元素，每列最多有  个非零元素；
• Win-Lose 表示收益矩阵每个元素为 0 或 1。

　　本文的主要结论为：

      1. 求解  -SWLP 的多项式近似纳什均衡点是 PPAD-Complete 的；
      2. 给出了求解  -SWLP 或  -SWLP 的精确纳什均衡解的高效（多项式）算法。

　　本文的主要结论通过改进前人证明框架得到，由于需要较多预备知识，请感兴趣的读者阅读原论文。

　　本文的主要贡献在于：

      1. 证明了即使在极度简化的多人博弈下，纳什均衡解计算仍然是困难的。这进一步质疑了纳什均衡解在多人情境下的预测能力；该结论对于基于纳什均衡解的多智能体增强学习（MARL）算法有引导作用；
      2. SWLP game 可以作为证明其他问题 PPAD-hard 结果的有用的规约起点。

　　最后，一个重要的尚未解决的问题是 constant sparse win-lose bimatrix game 的纳什均衡解计算复杂度。这一问题目前的最优结果由 Zhengyang Liu 与 Ying Sheng 在2018年得到，他们证明了 logarithmic sparse win-lose bimatrix game 的纳什均衡解是 PPAD-Complete 的。然而，得到更强的常数稀疏可能需要新的证明技巧。