2020年12月9日，智利大学教授 Jose Correa 带来了题为《采样数据中的最优停止算法》的主旨报告。报告由北京大学前沿计算研究中心邓小铁教授主持。

Jose Correa教授报告中

　　在生产生活中，经常会遇到这样的一类问题：有一些数据会依次到来，你需要在每个数据到来的时候做出决定，但在做出决定的时候是看不到之后的数据的。这样的具有不决定性的决策问题在许多领域有独特的应用。

　　这样的一类在线决策问题在经济学、金融、资源分配中都有着广泛应用。在实际生活中，在招聘甚至相亲中也有应用例子，例如天文学家开普勒面试第二任妻子的场景就可以被这个模型所刻画。

　　在线选择问题的核心难点在于做出选择时你无法预计到后面没有看到的情况，因此我们可以使用先知不等式（prophet inequality）来评价一个在线算法的好坏。所谓先知不等式，就是假设有一个先知能提前预知所有的输入，并在输入已知的情况下做出决策。一个在线算法的评价标准就是看这个在线算法能够以多大程度近似先知的决策。

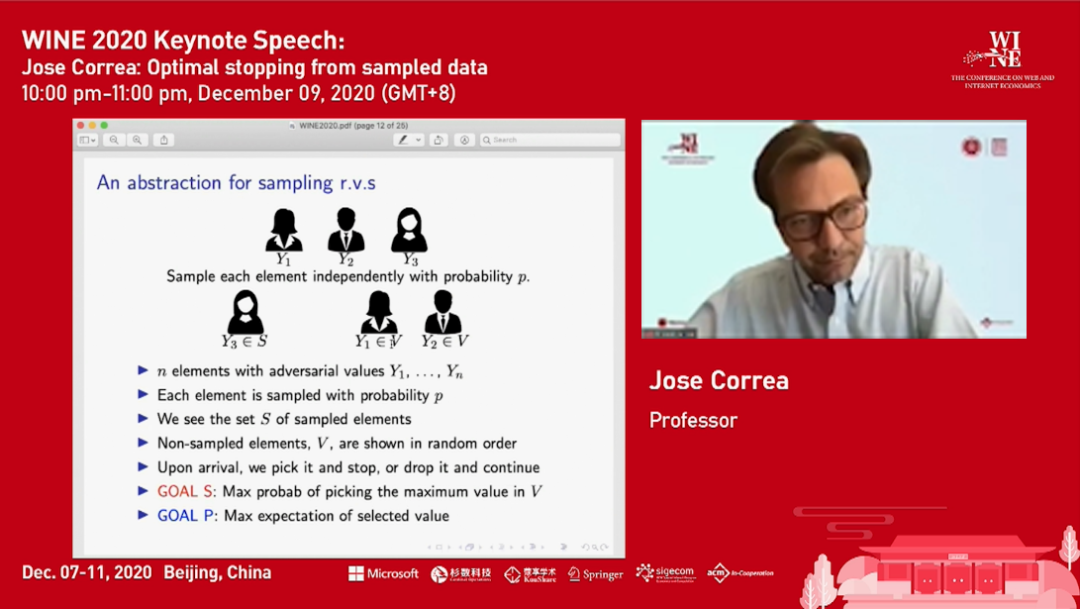
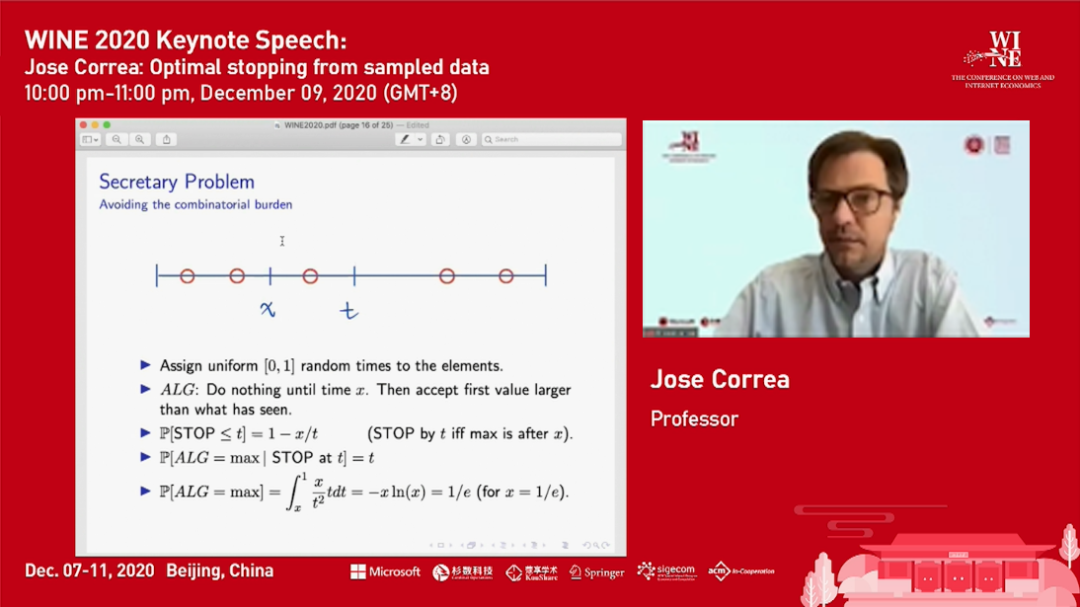
　　在线决策问题中有两大经典问题。一是秘书选择问题（secretary problem），有一系列候选人会依次来到，每次在一个秘书到来的时候，你可以看到她/他的能力值，然后选择或放弃这个秘书。一旦选择了某个秘书，就不能再看到之后的候选人了，如果放弃了某个候选人也不能再选择她/他了。我们需要设计的算法的目标是尽可能地选到最好的秘书（能力值最高）。

　　第二个问题是先知问题（prophet problem）。这个问题和秘书选择问题类似，不同点在于，目标并不是选择最好的秘书，而是使最后选择的秘书的期望能力值尽可能高。

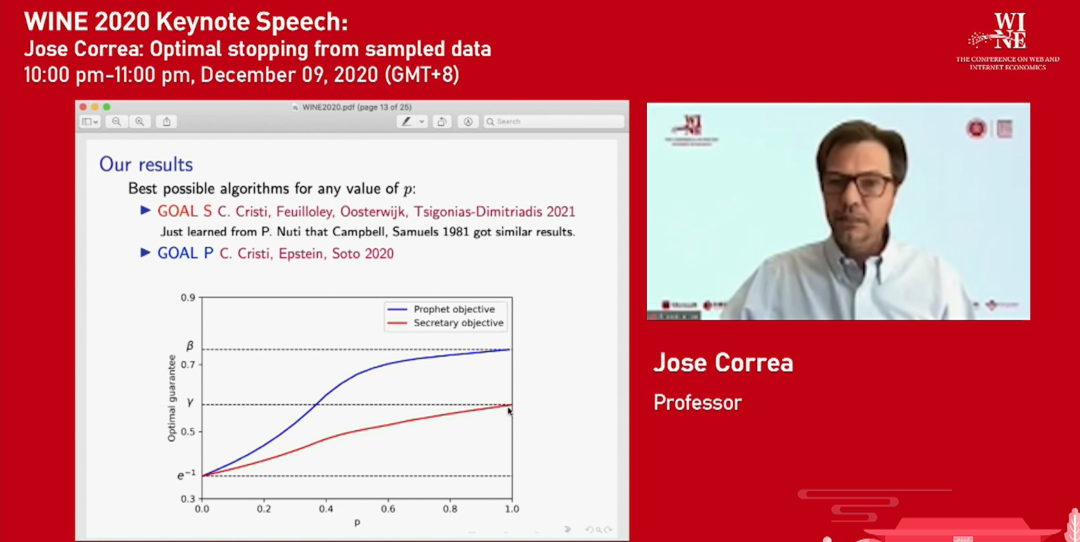
　　在这两个问题的经典假设中，这些输入要么是从已知分布中随机的，要么是完全任意的。而讲者这次的工作将这些模型组合了起来，定义了一个新的模型。该模型有一个参数 p，代表了这些输入有多大程度是随机的。当 p=0 时，该模型就变为了任意输入的情况，而 p=1 时，该模型就变为了已知分布的情况。

　　对于这个模型，作者在秘书选择问题和先知问题中分别给出了一个算法，并证明了对于秘书选择问题，该算法是最优的；证明了对于先知问题的算法在某个类型的算法中是最优的。作者还给出了两个算法在不同 p 的选取下的性能，可以看到，作者的算法在 p=0 或 p=1 时和经典的最优算法取得了完全相同的表现。