2019年6月11日，威斯康辛麦迪逊大学的蔡进一教授受邀访问北京大学前沿计算研究中心，在静园五院做了题为“Classification Program for Counting Problems”的主题报告，介绍了计数问题下的复杂性分类计划的进展。报告由中心讲席教授邓小铁主持，听众包括来自北京大学信息学院、数学学院的师生。

蔡进一教授报告现场

　　蔡老师先举了一些计算相关的问题的例子，包括解不定方程，大数分解。这一类问题解决可能很麻烦，但验证一组解的正确性比较简单。蔡老师随后引出了NP这一概念，在计算模型下概括了多项式时间可验证的一类问题。作为决策性问题，NP问题一般会问有没有一组满足条件的解。与NP这一决策性复杂类相对应的是#P这一计数版本复杂类，在这一类问题中，我们需要计算满足条件的解的个数。一个经典的例子是计算0-1矩阵A的积和式（Permanent），定义如下：

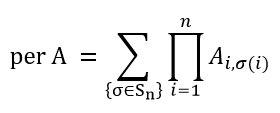
　　这一式子直观上给出了所有的置换对应的矩阵元素的乘积之和，一个简单的应用就是计算二部图的完美匹配的个数。积和式的计算为#P完全的。

蔡进一教授报告中

　　随后蔡老师提到了计数问题的复杂性分类计划，即对可以表示为积和式的一大类计数问题，给出分类条件，使得满足条件的问题是多项式可解的，否则就是#P难的。这里面值得注意的是，有些问题对于一般图是#P难的，但对于平面图，这些问题又是多项式可解的。比如著名的Kasteleyn算法，可以在多项式时间内计算平面图中完美匹配的个数，具体分析可以参见他和陈汐老师写的书《Complexity Dichotomies for Counting Problems》。蔡老师接着介绍了三种计数问题描述框架：图同态，计算满足限制问题（CSP）的解，Holant问题，并详细介绍了在这三类计数问题描述框架下，计数问题的复杂性分类的进展。

　　对于图同态框架，蔡老师以图染色问题为例，给出了图k-染色问题计数的配分函数（Partition Function）用于计算满足条件的染色个数。给定一个大小为k×k的矩阵，主对角线均为0，其余位置均为1，对图上的点染色后，对应的每条边做一个判断，边的两端在矩阵的位置是否为1，这些判断的乘积即给出了一个染色是否是合法的，而枚举所有的染色方案算得相应的积和式，可以给出图染色问题的计数个数。对于其他问题，也有类似的对应方案把问题放在图同构框架下描述。这一模型下有诸多的二分（dichotomy）结论，即满足给定条件的问题是多项式可解的，否则就是#P难的。这一系列的工作源自Dyer和Greenhill，他们给出了{0,1}域上的二分定理，Bulatov和Grohe将其推广到非负域上，Goldberg等人将其推广到实值域上，最终蔡进一、陈汐、陆品燕将这一问题推广到复数域上，基本上完美地解决了这一问题。这一框架下的公开问题是对于度数有限的情况，给出分类条件。蔡老师和其学生最近在度数有限的场景下有突破性进展，相关论文正在撰写中。

　　蔡老师随后介绍了CSP框架，这一框架将问题概括为约束满足问题，并同样计算所有的赋值下，对应的配分函数的值，得到对应问题的计数个数。相关的二分定理也有很多，蔡老师重点提到了这里面可以做到三分的工作，即分为多项式可解，平面图多项式可解一般图#P难，平面图#P难。这一系列的结果包括对称实值限制函数下的分类条件，对称复值限制函数下的分类条件，复值函数下的分类条件。蔡老师称，这些工作证明的完成，除了巧妙的构造想法以外，也需要大量的计算验证。

　　最后蔡老师介绍了Holant框架，这一框架更为通用，而上述的CSP框架后来被发现是Holant框架的特殊形式。蔡老师提到，这一框架下的分类问题，虽然也有诸多进展，但还有很多悬而未解的问题。

蔡进一教授与邓小铁教授合影

　　在报告的最后，蔡老师花了一些时间向同学们展示了他们证明二分定理用到的部分技术，包括一些很有对称性质的部件构造（用于将复数化为实数），范德蒙矩阵系统等。被问到如何想到这些精妙的构造时，蔡老师称，他们也是做了很多尝试的，但这些尝试基于一个原则，即构造的部件必须看起来很优美，不优美的构造一般来说是不管用的。报告结束后，邓小铁老师代表中心送给蔡进一老师纪念品，接下来，蔡老师还和中心的师生一起进行了座谈交流。