首届国际理论计算机联合大会（International Joint Conference on Theoretical Computer Science，IJTCS）于2020年8月17日-22日在线上举行，主题为“理论计算机科学领域的最新进展与焦点问题”，由北京大学与中国工业与应用数学学会（CSIAM）、中国计算机学会（CCF）、国际计算机学会中国委员会（ACM China Council）联合主办，北京大学前沿计算研究中心承办。  

　　8月17日，大会“算法博弈论”论坛如期举行，苏州科技大学程郁琨教授和上海财经大学唐志皓助理教授共同主持。小编为大家带来论坛精彩回顾。

Envy-freeness up to Any Item with High Nash Welfare
Nick Gravin，上海财经大学

　　本次报告是关于不可分割物品分配的公平性和高效性的问题。首先，讲者介绍了相关背景知识，和问题的设定情景，结合例子解释了刻画分配公平性的重要概念——envy-free（EF）、envy-free up to one item（EF1）和 envy-free up to any item（EFX），和刻画高效性的重要概念——纳什福利（Nash Welfare）和帕雷托最优（Pareto Optimality）。同时他指出 EF 不一定存在，EF1 总是存在，而 EFX 目前只知道特殊情景下的存在性。接着，他用一个例子强调在 EFX 的公平分配下也可能会有很低的纳什福利，这也正是论文要探索和解决的问题。

　　关于这个问题，讲者先说明了局部 EFX 分配（partial EFX allocation）的想法，如将部分物品捐给慈善机构等可能性，然后讲者分享了三个成果。第一个是总存在局部 EFX 分配使得它的纳什福利至少是最优纳什福利的1/2，并且该分配是帕雷托最优的；另外，这里的1/2是紧的，即存在一种情形使得任何 EFX 分配的纳什福利都不超过最优纳什福利的1/2。第二个是在大市场条件下，即每个物品的价值相对于整个市场中物品总价值而言足够小，此时存在局部 EFX 分配使得它的纳什福利足够接近最优纳什福利。第三个是找到上述局部 EFX 分配的算法。

Fair Division of Mixed Divisible and Indivisible Goods
贝小辉，南洋理工大学

　　如何公平地分配资源一直是一个研究的热门话题。相关研究的模型可以分为两个类别：其一，假设资源是多种多样并且无限可分的，也就是 cake cutting 问题；其二，假设资源是不可分割的。对前者而言，公平性由 envy-freeness（EF）刻画，即相比于别人得到的物品，每个参与者都更喜欢自己的那一份；而对后一种假设而言，EF 性质可能不存在，因此被放宽为 envy-freeness up to one good（EF1）：如果从别人的物品中移走一种，那么所有人都更喜欢自己的那一份物品。在此基础上，讲者考虑了一个更加现实的模型——资源是混合的，既包含可分的也包含不可分的。相应的，讲者也将 EF 和 EF1 融合为 envy-freeness for mixed goods（EFM）。直观地说，EFM 要求对于每个参与者，如果其份额中仅包含不可分割的资源，则其他人将使用 EF1 标准进行比较；但如果参与者分到了可分割的资源，则其他人将使用更严格的 EF 标准进行比较。

　　讲者证明了对于任意数量的参与者始终存在 EFM 分配，并根据是否存在 oracle 分别给出了算法，最后讨论了如何在 Robertson-Webb 模型下用多项式时间内找到 ε-EFM 近似的分配。

Truthful Mechanisms for Location Games of Dual-Role Facilities
陈旭瑾，中国科学院数学与系统科学研究院

　　在 Facility Location Game（FLG）中，政府要根据用户的位置选择公共设施的建造地点，而设施与用户的距离决定了用户要支付的费用。在传统模型中，用户的位置是私有的信息，因此用户可以有策略地上报自己的位置来减少需要支付的费用，而政府是无策略的，并且建造设施的地点是任意的。但在现实场景中，建造地点也需要在几个预先公开的场地中选择一个或多个，同时还往往要考虑政府的财政收入。因此，讲者提出 Dual-Role FLG（DFLG），将政府和用户统一为有策略的 agent，这些 agent 的位置是公开的。每个 agent 都是潜在的设施建造者，同时他们各自的建造成本是私有信息。当一个 agent 成为建造者时，会产生建造成本同时对其他 agent 收费。因此，agent 的收益是其收取的服务费减去成本，而每个 agent 可以通过有策略地上报自己的成本来提高收益。

      在此基础上，讲者研究了真实机制设计，并有如下结果：
      1. 当目标为最小化最大费用时，给出了多项式时间的最优真实机制。
      2. 当目标为最小化总费用时，给出了 individually rational 并且 normalized（不是建造者的 agent 收取费用为0）的真实机制；以及一个多项式时间，近似比为1.61的近似算法。

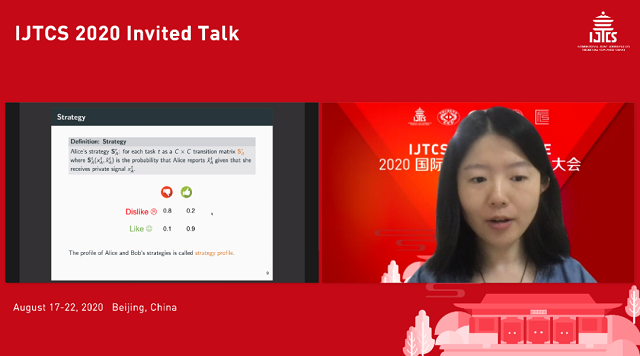
Dominantly Truthful Multi-task Peer Prediction with a Constant Number of Tasks
孔雨晴，北京大学

　　同伴预测是日常生活中常见的问题，例如发放调查问卷时，需要设计合理的机制鼓励回答者填写其真实的倾向。其挑战在于需要在尽可能少的先验知识和预设下，设计实际可行的真实（truthful）机制。过去的工作或者真实性是近似的（ε-δ truthfulness），或者需要无穷多次询问。

　　在该工作中，讲者在通常的框架下，设计了一种基于行列式的互信息函数。讲者证明了该函数对询问结果所提供的信息量是单调的，并用常数次询问获得了该互信息函数的一个无偏估计作为回报函数，得一真实机制，对过去的工作作出了突破式的改进。最后，讲者还根据该机制设计了一个 scoring rule，后者还可用于机器学习中，设计对标签噪音鲁棒的损失函数。

Data-driven Auctions, Prophet Inequality, and Pandora's Problem
黄志毅，香港大学

　　在机器学习理论领域，算法的样本复杂度是一个重要的研究方向。它代表了我们需要提供给该算法的训练样本的数量，从而算法才能在一组函数中寻找到一个几乎最优的函数。近年来，在贝叶斯优化问题（Bayesian Optimization Problem）的样本复杂性也逐渐被大家所重视。其中，关于拍卖（Auctions），先知不等式（Prophet Inequality）和潘多拉问题（Pandora's Problem）已有一系列研究。在先前的研究中，人们对这些问题的样本复杂性研究是基于具体问题单独分析的。此报告首次给出了一个通用方法，在三个问题的样本复杂度上都得到了最优或是接近最优解。

　　具体地，讲者关注了高维数据点满足乘积分布，即数据的不同维度之间独立的情况。分析主要分为三步进行，把对于数据集的假设逐步放宽。首先对于数据集有界且支撑集有限的情况，讲者得到的结论可直接推广，得到多物品拍卖问题的最优样本复杂度。第二步，讲者把支撑集有限的假设替换为强单调性，其中强单调性是以上三个问题均满足的性质。在这个条件下，得到的结论可以直接推出单物品拍卖、先知不等式和潘多拉问题接近最优的样本复杂度。最后一步，将有界的条件去掉，得到的结论能直接推出在分布无界情况下的单物品拍卖、先知不等式和潘多拉问题接近最优的样本复杂度。