近日，北京大学计算机学院前沿计算研究中心助理教授李彤阳课题组在无权图上高斯玻色采样（Gaussian Boson Sampling，GBS）分布高效经典采样算法研究方面取得重要进展。研究团队提出了一种基于马尔可夫链蒙特卡洛（MCMC）的“双循环Glauber动力学”采样算法，在理论上首次证明该算法可在多项式时间内高效生成与量子玻色采样分布一致的样本。相关成果以《无权图上高斯玻色采样分布的高效经典采样》（“Efficient Classical Sampling from Gaussian Boson Sampling Distributions on Unweighted Graphs”）为题发表于国际知名期刊《自然-通讯》（Nature Communications）。

图1 论文截图

高斯玻色采样是当前验证量子计算潜在优势的重要模型之一，其计算复杂度与图论中一种名为hafnian的数学量密切相关。hafnian直接反映了图中完美匹配的数量，因此高斯玻色采样不仅是量子物理实验的关键问题，也在最密子图、组合优化等图论任务中具有重要意义。

然而，现有针对GBS的经典模拟方法普遍存在计算开销巨大、缺乏普适性能保证等瓶颈。如何在理论上构建一个既能匹配量子分布又具备可证明效率的经典算法，是长期未解的难题。

针对这一问题，李彤阳课题组聚焦无权图这一具有重要理论意义的场景，提出了双循环Glauber动力学（Double-loop Glauber Dynamics）算法。该算法在传统马尔可夫链采样的外层迭代中，引入内层链在导出子图上近似均匀地采样完美匹配，从而将采样分布的权重从与hafnian成正比提升至与hafnian的平方成正比，实现了与高斯玻色采样分布的精确对齐。

在理论分析方面，团队还利用改进的正则路径（canonical path）方法，严格证明该算法在稠密图上能够在多项式时间内混合收敛，为经典算法高效模拟量子分布提供了新的数学工具。

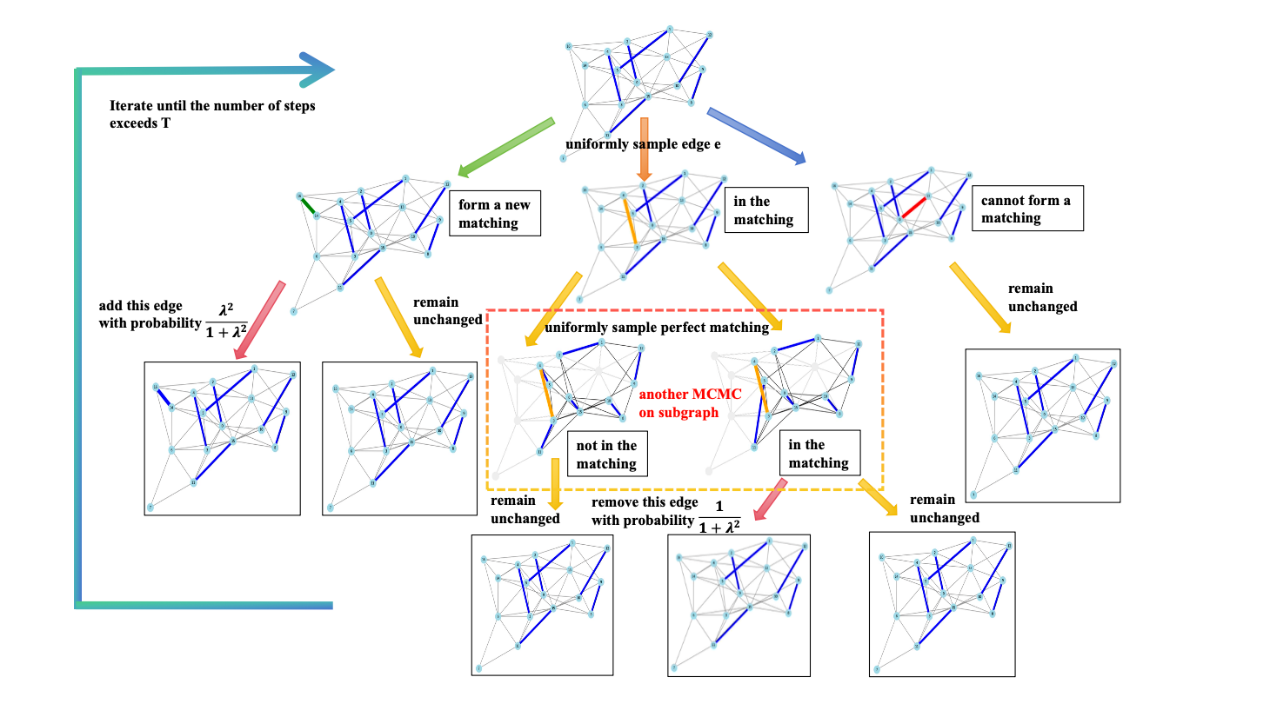
图2 双循环Glauber动力学流程图

在应用验证层面，研究团队开展了大规模数值实验，在256顶点的图上求解最大Hafnian和最密k-子图问题，其规模超越了此前的GBS实验及相关经典模拟研究。相较原始随机搜索与模拟退火框架，双循环算法将求解质量最高提升至10倍，团队还进行了系统的误差与收敛分析，充分验证了理论的有效性，并展现了算法的实际优势。

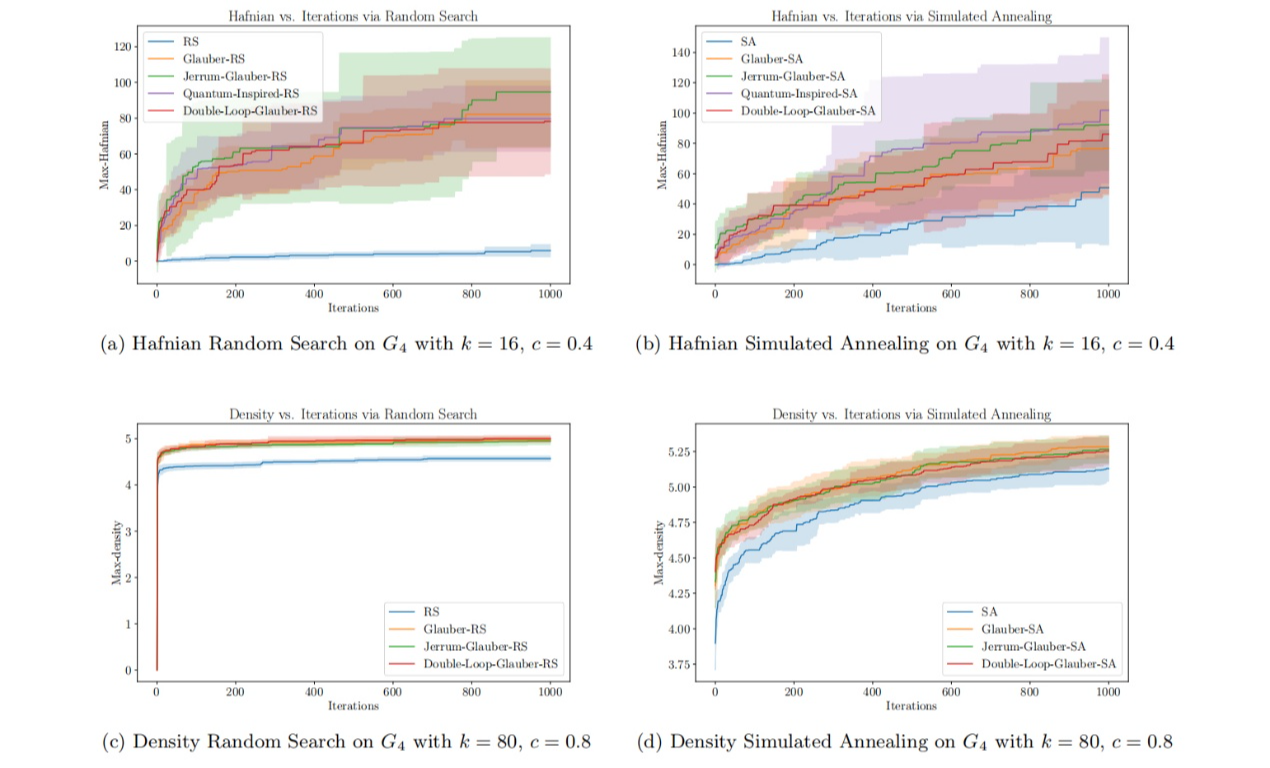
图3 双循环Glauber动力学实验

该项研究在理论上给出与GBS分布的一致性与多项式混合性保证，在实践上提供可扩展的经典基准，有助于客观评估光量子体系在图优化问题上的潜在优势，并为相关组合优化与采样问题提供可复用的方法学框架。

北京大学博士生张业鑫、周烁、王昕兆为研究论文共同第一作者，王紫若、杨子熠、杨睿、薛烨诚均对该工作有所贡献，李彤阳为该论文的通讯作者。该研究得到了国家自然科学基金的支持。