CFCS Quantum Day, organized by Center on Frontiers of Computing Studies (CFCS), Peking University, was held virtually on May 12th, 2021. Top-level researchers in quantum computing were invited as speakers and gave stimulating talks (videos can be accessed here). Nearly 5000 people from universities such as Tsinghua University, University of California, Berkeley, Purdue University, Duke University, University of Maryland, EPFL participated the event via live streaming platforms. Prof. Zhengfeng Ji from University of Technology Sydney, and Dr. Xiao Yuan, Dr. Kuan Cheng, and Dr. Tongyang Li from CFCS, Peking University co-hosted the talks.

 

Prof. Baoquan Chen, executive director of CFCS, welcomed everyone for attending CFCS Quantum Day in his opening remarks, and sincerely expected inspiring academic exchanges.

 

 

Talk Information

 

1. Fast Simulation of Planar Clifford Circuits

 

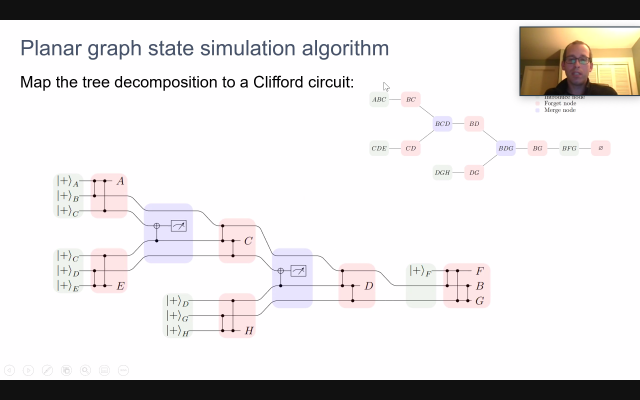
Prof. David Gosset, University of Waterloo

Abstract

Clifford circuits are a special family of quantum circuits that can be simulated on a classical computer in polynomial time using linear algebra. Recent work has shown that Clifford circuits composed of nearest-neighbor gates in planar geometries can solve certain linear algebra problems provably faster--as measured by circuit depth-- than classical computers. We don't know if these linear algebra tasks also admit polynomial quantum speedups in terms of total runtime (gate complexity). Motivated by this question, here we show that treewidth and planarity can be used to improve classical algorithms for simulating Clifford circuits. Our main result is a classical algorithm with runtime asymptotically upper bounded as n^{W/2} which samples from the output distribution obtained by measuring each qubit of a quantum planar graph state in given Pauli bases, where W is the matrix multiplication exponent. We also provide a classical algorithm with the same asymptotic runtime which samples from the output distribution of any constant-depth Clifford circuit in a planar geometry. This is joint work with Daniel Grier, Alex Kerzner, and Luke Schaeffer (arxiv:2009.03218).

 

2. Efficient Quantum Algorithm for Dissipative Nonlinear Differential Equations

 

Prof. Andrew Childs, University of Maryland

Abstract
While there has been extensive previous work on efficient quantum algorithms for linear differential equations, analogous progress for nonlinear differential equations has been severely limited due to the linearity of quantum mechanics. Despite this obstacle, we develop a quantum algorithm for initial value problems described by dissipative quadratic ordinary differential equations. We also establish lower bounds on the worst-case complexity of quantum algorithms for nonlinear differential equations, identifying cases in which the problem is intractable.

This talk is based on joint work with Jin-Peng Liu, Herman Kolden, Hari Krovi, Nuno Loureiro, and Konstantina Trivisa.

 

3. The Quantum Complexity of the Closest Pair Problem

 

Dr. Chunhao Wang, Pennsylvania State University

Abstract
Given n points in a d-dimensional space, the goal is to find a pair of points with the smallest distance. In constant dimensions, we knew the classical upper/lower bounds and a quantum lower bound. When the dimension goes up to polylog(n), we knew classical upper and (conditional) lower bounds, as well as a quantum upper bound. In this talk, I will introduce the quantum upper bound of this problem in constant dimensions and the (conditional) quantum lower bound in polylog(n) dimensions. Both the bounds are tight (up to some poly-logarithmic factor). The upper bound (quantum algorithm) is based on quantum walk search, and the lower bound is based on quantum fine-grained reductions and a quantum version of the strong exponential-time hypothesis.

The talk is based on arXiv:1911.01973 and it will be accessible to a general computer science and mathematics audience without a quantum computing background.

 

4. Quantum Algorithms for Semidefinite Programs with Applications to Machine Learning

 

Dr. Tongyang Li, Massachusetts Institute of Technology and Peking University

Abstract
Semidefinite programming has been a central topic in the study of mathematical optimization, theoretical computer science, and operations research in the last decades. In this talk, we introduce a quantum algorithms for solving SDPs with polynomial speedup compared to the best known classical algorithms. We also introduce how the quantum algorithm can be applied to training linear and kernel-based classifiers, as well as solving general matrix games. The talk is based on three papers: https://arxiv.org/abs/1710.02581, https://arxiv.org/abs/1904.02276, and https://arxiv.org/abs/2012.06519.

 

5. Recent Advances in Predicting Properties of Quantum Systems

 

Hsin-Yuan Huang, California Institute of Technology

Abstract
I will present a rigorous and efficient procedure for converting a quantum system into a succinct classical description of the system, its classical shadow. Classical shadows can efficiently predict many properties of interest, including expectation values of local observables and entanglement entropy in local subsystems. Recently, progress has been made in experimentally realizing the procedure and extending the capability of classical shadows. For example, in an ongoing work, we show that efficient classical machine learning algorithms using classical shadows can address quantum many-body problems, such as classifying phases of matter.

 

6. Fluxonium Qubits for Ultra-high-fidelity and Scalable Quantum Processors

 

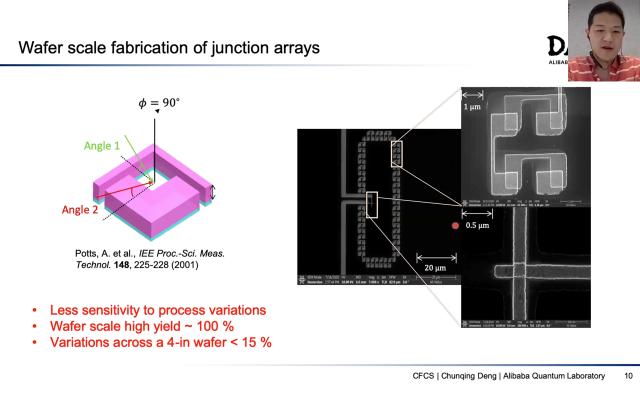
Dr. Chunqing Deng, Quantum Scientist and Head of the Experimental Group, Alibaba Quantum Laboratory

Abstract
The success of superconducting quantum computing (SQC) has so far been largely built upon the transmon qubit. Finding an alternative qubit that drastically outperforms transmon represents one of the most fundamental and exciting frontiers of SQC. The fluxonium qubit stands out as a promising candidate, due to its long coherence times and large anharmonicity. Furthermore, fluxonium can be directly integrated into the existing circuit-QED schemes for scaling. For these reasons, fluxonium is our qubit platform of choice at Alibaba Quantum Laboratory.

In this talk, I will present our design and experiments of a 2D fluxonium circuit, which exhibits high coherence, high tunability and strong coupling. With T1 and T2 > 100 us at around the sweet spot, we achieve a dielectric loss tangent as low as 0.7e-6, approaching the state of the art. Using a high-bandwidth flux bias, we demonstrate robust qubit reset and readout, together with fast one- and two-qubit gates. In particular, we realized an iSWAP two-qubit gate, achieving 0.995 fidelity. Our work paves the path toward a fluxonium-based, ultra-high-fidelity multi-qubit processor.

 

7. Computation with Tensor Networks

 

Prof. Pan Zhang, Chinese Academy of Sciences

Abstract
In this talk, Pan Zhang will present methods and algorithms for solving statistical mechanics problems, combinatorial optimization problems, and quantum circuit simulations, in an integrated framework based on tensor networks.

In statistical mechanics problems, the partition function (i.e. the normalization factor of the Boltzmann distribution) at a finite temperature can be obtained by contracting a tensor network that is converted from the stat. mech. problem. When equipped with the "Tropical" algebra, the tensor network contraction can be used to obtain ground state energy and entropy of the model directly at zero temperature. When the interactions in the stat. mech. model are complex, computing the partition function acts as estimating the amplitude of an end state basis vector of a quantum circuit, thus tensor network contractions can be used to simulate quantum circuits. Pan Zhang will introduce approximate and exact algorithms for contracting tensor networks, and their wide applications, particularly in simulating Google's Sycamore quantum circuits.

 

8. Quantum Simulation with Hybrid Tensor Networks

 

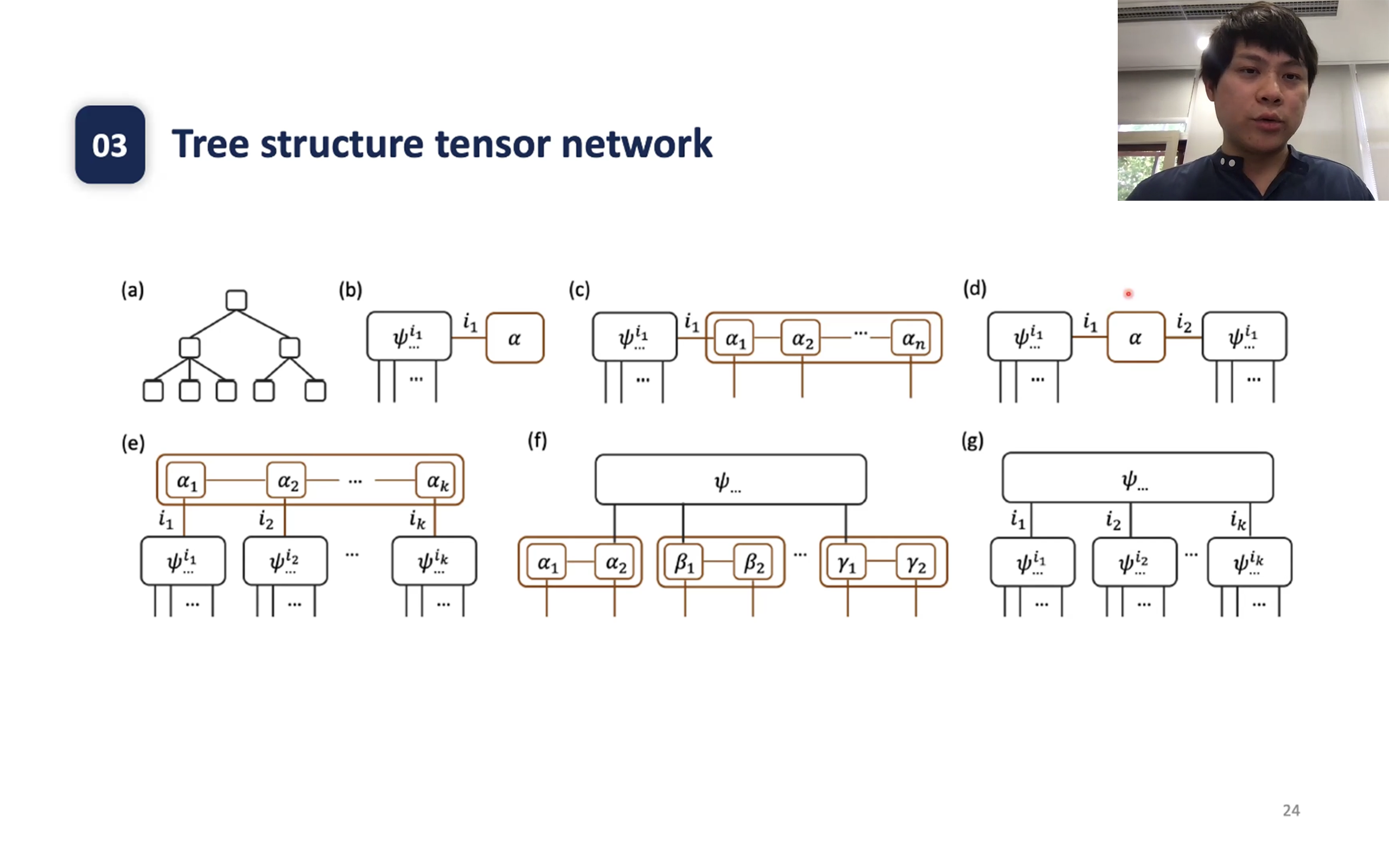
Dr. Xiao Yuan, Peking University

Abstract
Tensor network theory and quantum simulation are respectively the key classical and quantum computing methods in understanding quantum many-body physics. Here, we introduce the framework of hybrid tensor networks with building blocks consisting of measurable quantum states and classically contractable tensors, inheriting both their distinct features in efficient representation of many-body wave-functions. With the example of hybrid tree tensor networks, we demonstrate efficient quantum simulation using a quantum computer whose size is significantly smaller than the one of the target system. We numerically benchmark our method for finding the ground state of 1D and 2D spin systems of up to 8*8 and 9*8 qubits with operations only acting on 8+1 and 9+1 qubits, respectively. Our approach sheds light on simulation of large practical problems with intermediate-scale quantum computers, with potential applications in chemistry, quantum many-body physics, quantum field theory, and quantum gravity thought experiments.

 

9. Photonic Quantum Computational Advantage

 

Prof. Chao-Yang Lu, University of Science and Technology of China

Abstract
The main challenge for scaling up photonic quantum technologies is the lack of perfect quantum light sources. We have pushed the parametric down-conversion to its physical limit and produce two-photon source with simultaneously a collection efficiency of 97% and an indistinguishability of 96% between independent photons. Using a single quantum dot in microcavities, we have produced on-demand single photons with high purity (>99%), near-unity indistinguishability, and high extraction efficiency—all combined in a single device compatibly and simultaneously. Based on the high-performance quantum light sources, we have implemented boson sampling—which is an intermediate model of quantum computing, a strong candidate for demonstrating quantum computational advantage and refuting Extended Church Turing Thesis—with up to 76 photon clicks after a 100-mode interferometer. The photonic quantum computer, Jiuzhang, yields an output state space dimension of 10^30 and a sampling rate that is 10^14 faster using the state-of-the-art simulation strategy on supercomputers.

 

10. Approximating Permanent of Random Matrices with Vanishing Mean

 

Prof. Zhengfeng Ji, University of Technology Sydney

Abstract
The algorithm and complexity of approximating the permanent of a matrix is an extensively studied topic. Recently, its connection with quantum supremacy and more specifically BosonSampling draws particular attention to the average-case approximation problem of the permanent of random matrices with zero or small mean value for each entry. Eldar and Mehraban (FOCS 2018) gave a quasi-polynomial time algorithm for random matrices with a mean of at least 1/polyloglog(n). In this talk, we will discuss how to improve the result, simplify the proof, and hopefully further motivate interests in understanding the central complexity theory conjectures supporting quantum supremacy claims. It is based on joint work with Zhihan Jin and Pinyan Lu.

 

About CFCS Quantum Day

 

 

CFCS Quantum Day, organized by Center on Frontiers of Computing Studies (CFCS), Peking University, is a one-day seminar focusing on pioneering works on supremacy, quantum simulation, and applications with near-term quantum computing hardware. Given continued uncertainty surrounding the future of COVID-19 and worldwide travel precautions, CFCS Quantum Day was held online on May 12th, 2021.